[LeetCode] 優化 LeetCode 的解答，與 hashmap 另類解法 #18 4Sum

- 6月 24, 2021

LeetCode 上第一個解答已經夠快了，一丟就 8ms，但我們有沒有辦法找出更快的解法?

Profile 看看問題出在哪

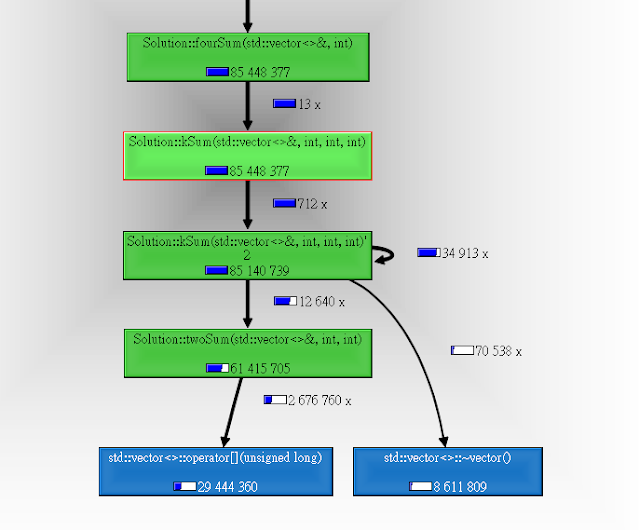
用 Callgrind profile 一下發現他花了很多力氣在存取 nums array 和 destruct vector 上:

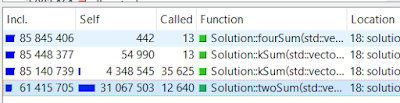
而且程式花了大部分的力氣在跑 twoSum:

看到 Self 那麼多 instructions 就代表大部分運算都卡在 twoSum。

所以如果我們想要優化這個解法，我們可以用以下任何手段來達成:

減少 nums 被存取的次數
減少 create vectors，這樣就間接減少了 vector<>::~vector() 的機會
盡量少呼叫 twoSum

如何先刪除重複的數字?

因為 input 有可能有重複的數字，所以其實我們很常這樣寫來跳過重複的數字:


if (... || nums[i - 1] != nums[i]) ...
if (... || (lo > start && nums[lo] == nums[lo - 1])) ...
if (... || (... && nums[hi] == nums[hi + 1])) ...

如果跑過 N 個數字，我們其實要存取 vector 2N 次，你可以用一個 variable 暫存上一個數字，可是你還是躲不過和上個數字比較。

可是我今天要介紹一個算是技巧嗎? 還是暴力解? 我們連比較都不用，因為我們把重複的數字都先刪掉了。

可是如果 input 有重複的數字，我們要怎麼輸出可能重複 2~4 次的數字?

窮舉重複數字

我們就先把這些答案先輸出就好了，想法就是我們把 4 個數字的各種多個數字重複的可能窮舉出來:

a + a + a + a = target
a + (b + b + b) = target
(b + b + b) + a = target
(a + a) + (b + b) = target
(a + a) + b + c = target
a + (b + b) + c = target
a + b + (c + c) = target
a + b + c + d = target

而且有一個條件 (requirement) 就是 a < b < c < d，因為不保持順序的話例如 #2 和 #3 就有可能會搞混 (e.g., a = 3, b = 1)。

那麼以上的 #1~#7 我們都可以用少於等於 O(N^2) 時間的演算法直接找到他，我們先統計 nums 所有數字的出現次數，然後再慢慢一個一個檢查:

直接把 target / 4 看 a 有沒有 4 個以上
For "a" in nums: 直接看 b 有沒有 3 個以上
For "a" in nums: 直接看 b 有沒有 3 個以上
For "a" in nums: 看 b 有沒有 2 個以上
For "a" in nums, for "b" in nums: c 有沒有 1 個以上
For "b" in nums, for "a" in nums: c 有沒有 1 個以上
For "c" in nums, for "a" in nums: b 有沒有 1 個以上

再來我們把重複的數字從 input 移除後再來跑 #8 我就可以跟你保證有 2 個數字以上重複的解答都已經被找完了，你不用再跳過重複的數字了。

這樣的程式碼想也知道又長又醜，所以我就丟在 GitHub 不放在文章中了。

簡化 LeetCode 的解答

移除掉重複的數字後我們就可以讓 twoSum 乾淨一點:


  std::vector<std::vector<int>> &twoSum(std::vector<int> &nums, int target,
                                        int start) {
    static std::vector<std::vector<int>> res;
    res.clear();
    int lo = start, hi = nums.size() - 1;
    int loNum = nums[lo], hiNum = nums[hi];
    int sum = loNum + hiNum;
    while (lo < hi) {
      if (sum < target)
        loNum = nums[++lo];
      else if (sum > target)
        hiNum = nums[--hi];
      else {
        res.emplace_back(std::initializer_list<int>{loNum, hiNum});
        loNum = nums[++lo];
        hiNum = nums[--hi];
      }
      sum = loNum + hiNum;
    }
    return res;
  }

再加上一些優化小技巧:

Line 3: 我們把 res 變成 static 這樣每次離開 twoSum 就被 destructed 下次又要再造一個
Line 14: 用 emplace_back + initializer_list 而不是 push_back 不然 vector 會先被造出來再被呼叫 move constructor 會浪費時間 (我一開始還用 emplace_back + std::vector<int>{...} 一懷疑去查 Google 就學到這樣其實還是會呼叫 move constructor)

減少 Recursion 呼叫次數

之前在 #16 有曾經說過兩個數字加起來所形成的數字範圍其實會像慢慢飄走的彩帶一樣慢慢往後走:

所以如果我們要找 target=160，有很多可能性其實我們可以忽略不算。

LeetCode 解答雖然有做到這件事，可是他只有在 kSum 一開始檢查範圍:


    if (start == nums.size() || nums[start] * k > target || target > nums.back() * k)
      return res;

檢查如果過了呢? 接下來跑 for loop 他就不檢查了。說不定接下來不管怎麼加都會超過 target，或是一開始怎麼加都不可能達到 target，但他還是會傻傻的 recursively 呼叫 kSum，然後才發現早就超過。

另外一個問題就是他檢查是不是超過範圍其實是粗估計算，所以有可能會白跑一些數字，但尾端的計算其實我們就可以稍微再精確一點，讓他少跑一些數字。

整體而言優化過的 kSum 就會長這樣:


  std::vector<std::vector<int>> kSum(std::vector<int> &nums, int target,
                                     int start, int k) {
    if (start == nums.size() || nums[start] * k > target ||
        target > nums.back() * k)
      return {};
    if (k == 2) return twoSum(nums, target, start);

    // Find k-1 largest sum in the tail
    int tailSum = 0;
    for (int i = nums.size() - (k - 1); i < nums.size(); ++i) {
      tailSum += nums[i];
    }

    std::vector<std::vector<int>> res;
    for (int i = start; i < nums.size(); ++i) {
      const int num = nums[i];
      // If so, the largest possible sum in this iteration will not >= target
      if (target > (nums[i] + tailSum)) continue;
      // If so, further sum would only get bigger
      else if (num * k > target)
        return res;

      for (auto &set : kSum(nums, target - num, i + 1, k - 1)) {
        res.emplace_back(std::initializer_list<int>{num});
        res.back().insert(std::end(res.back()), std::begin(set), std::end(set));
      }
    }
    return res;
  }

少跑一些 kSum 就會間接少跑一些 twoSum。

優化完再 Profile

我們就會發現 twoSum 的 instructions 的數量從 31M 減少為 22M:

Call graph 呼叫次數和 instructions 也少掉很多:

vector [] 存取次數少了一半
第二次 kSum 呼叫次數少了一半
kSum 和 twoSum 的 instructions 總數量都少了一半

不過 submit 完結果還是和原本一樣 8ms:

難道優化沒用? 其實不是。

是因為這題的測資過於簡單，雖然他說 input 最多 200 個，但我去偷看其實超過 100 的測資只有 1 組，大部分測資都超級短，所以優化的效果這邊並看不出來。

自己來 Benchmark

我們當然可以自己產生比較大的測資，來看看優化前與優化後到底有沒有差異，於是我就做了一個 benchmark program:

基本上 scale 兩倍產生出來的 input 長度也會變兩倍。

kSum 是優化前，kSum Optimized 是優化後的版本。我們可以很明顯看到當 scale=10 優化後的版本比沒優化的少了 1.5 秒左右。

完整優化版本的程式碼其實也很長，所以我就只放 GitHub 上了。

其他做法 1: O(N^2) Hashmap

其實我有印象這一題在上某堂程式課的時候有提到可以用 O(N^2) 的方式直接做掉，簡單來說就是先把兩個數字的各種可能先寫在 map 上，之後再把兩個數字相加看答案在不在寫好的 map 裡面。

詳細作法其實已經有文章在介紹了，就容我這邊跳過不做介紹。

不過寫出來的時間可是慘兮兮，大概也是這一題為什麼幾乎都看不到有人推薦這個做法:

原因和 #15 一開始遇到的問題一樣，就是 STL containers 找東西太花時間了。

優化: O(N^2) Hashmap + Two Pointers

因為 Hashmap 破壞了我們從左往右依序找東西的順序，我們很難知道現在找到 a + b + c + d = target 的四個數字是不是已經有人 output 過了，所以通常我們就會用這樣的方式去存 output:


std::set<std::vector<int>> output;

不過問題是每次要丟東西進去都要和舊的東西 compare 一下，越多 output 這個解法其實會越慢。最後我們還要把它轉回 vector!

有沒有什麼辦法可以讓 STL contains 紀錄的東西不要那麼複雜?

於是我就想到一個很簡單的方式:

對於同一個 sum = a + b，我記錄 a 和 b 的 index，越往左邊靠的越好，而且只記一組 (a, b)
對於同一個 sum = a + b，我記錄 a 和 b 的 index，越往右邊靠的越好，而且只記一組 (a, b)

到時候例如 c=50, d=30, target=100, 我找到有人 (a+b) = target - (c+d) = 20，但我不知道到底有多少組 a+b = 20，沒關係我就用兩個 for loop 加上 two pointers 慢慢把其他同樣總和是 20 的 (a, b) 找出來。

優點是我可以避免重複數字的問題。缺點是我要多花時間去跑。

完整的 C++ 程式碼就請看 GitHub。

其他做法 2: Binary Search kSum

在 #16 最後"進階優化" 我有提到其實我們可以用 binary search 直接找到要搜尋的範圍，4Sum 看起來這麼難我們當然要試試看能不能有幫助。

第一個寫法就是先把最小和最大的範圍都先用 vector 算好，再去 binary search。不過這樣我們就浪費力氣算一些 binary search 會跳過的地方。

所以第二個寫法就是改良一下，我們在 binary search 跑到的地方再去算值，不過程式碼就滿醜的。

這個做法我沒擺上來 benchmark 的原因是我發現優化後的版本竟然和 kSum 跑的一樣快! 而且還是不分上下那種。仔細分析發現大部分時間都耗在 twoSum，所以我跳過的地方其實占比非常小。

kSum, Hashmap 大 PK

我們把 kSum 和 Hashmap 以及他對應的優化版本全部放上來就會發現很有趣:

O(N^3) kSum 和 O(N^2) Hashmap 差不多快
優化後的版本也是不分上下

不過差距看起來還是很小，如果我們再把 scale 繼續放大會怎麼樣呢?

結果就會發現 hashmap 解法在資料越多的時候優勢就會慢慢的展現出來:

不過我比較訝異的是 hashmap + two pointers 我原本沒有預期他會是最快的，看起來會比純 hashmap 再快一些。

結語

其實一開始是想要想出一些奇異解法來贏過 LeetCode 官方的解答，可是怎麼就是贏不了。後來想說乾脆來幫他優化好了，成功的話還可以寫一篇文章，所以你才看的到這篇文章。

上面幫 kSum 優化的作法其實是我一開始覺得最沒什麼用的做法，我花了很多力氣想要拯救 hashmap 作法，可是只要牽扯到 STL containers 就會滿慢的所以後來才意外和移除重複數字的作法結合在一起。

有時候比較差的做法換個角度，說不定真的會有什麼用。

搜尋此網誌

Clean Code Craving