Clean Code Craving

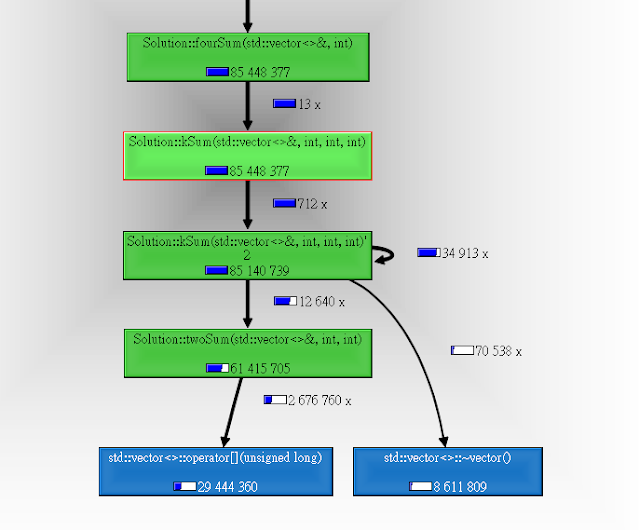
LeetCode 上 第一個解答 已經夠快了，一丟就 8ms，但我們有沒有辦法找出更快的解法? Profile 看看問題出在哪 用 Callgrind profile 一下發現他花了很多力氣在存取 nums array 和 destruct vector 上: 而且程式花了大部分的力氣在跑 twoSum : 看到 Self 那麼多 instructions 就代表大部分運算都卡在 twoSum 。 所以如果我們想要優化這個解法，我們可以用以下任何手段來達成: 減少 nums 被存取的次數 減少 create vectors，這樣就間接減少了 vector<>::~vector() 的機會 盡量少呼叫 twoSum 如何先刪除重複的數字? 因為 input 有可能有重複的數字，所以其實我們很常這樣寫來跳過重複的數字: if (... || nums[i - 1] != nums[i]) ... if (... || (lo > start && nums[lo] == nums[lo - 1])) ... if (... || (... && nums[hi] == nums[hi + 1])) ... 如果跑過 N 個數字，我們其實要存取 vector 2N 次，你可以用一個 variable 暫存上一個數字，可是你還是躲不過和上個數字比較。 可是我今天要介紹一個算是技巧嗎? 還是暴力解? 我們連比較都不用，因為我們把重複的數字都先刪掉了。 可是如果 input 有重複的數字，我們要怎麼輸出可能重複 2~4 次的數字? 窮舉重複數字 我們就先把這些答案先輸出就好了，想法就是我們把 4 個數字的各種多個數字重複的可能窮舉出來: a + a + a + a = target a + (b + b + b) = target (b + b + b) + a = target (a + a) + (b + b) = target (a + a) + b + c = target a + (b + b) + c = target a + b + (c + c) = target a + b + c + d = target 而且有一個條件 (requirement) 就是 a < b < c <...

上一篇我們用 數學分析讓 3Sum 快 2 倍 ，這題也有辦法用數學加快嗎? 當然可以。 為什麼 Two Pointers 可以這樣用? 在數學分析前我們還是要來先了解一下為什麼 two pointers 會有用，如果只知道用卻不知道為什麼可以這樣用，面試時簡單問一句就會被考倒。 答案很簡單，如果我們要找比較小的數字，移動錯指標的話完全沒有幫助: 同理如果我們要找更大的數字，移動指到比較大的數字的指標也沒有幫助: 這其實和 LeetCode #11 的移動原理 非常像。 什麼時候根本不用跑 Two Pointers? 如果第一個數字 A 固定的話，A+B+C 最小和最大的數值會是一開始跑和準備結束的時候: 如果我們想要找 A+B+C ≈ 300，中間的結果一定介於 [60, 180] 之間，我們幹嘛去跑 two pointers? 我們其實只要算一下最小和最大的可能性就可以決定要不要用 two pointers。 如果之後 A 固定住，我們要找 B+C ≈ 200，同理我們也可以先算最小和最大值來決定要不要跳過: 像這個例子 LeetCode 第二個解答就用 binary search，那我們知道範圍的話連跑都不用跑。 最後一個要提的陷阱就是我們可能會以為 wow 這樣做是不是 O(N) 因為我們可以直接找到 A 在哪裡，然後就去找 B+C 也是 O(N)。 但其實不是，因為我們可能會發現要找的目標可能會在很多範圍內: 而且我們也沒辦法事前知道我們要跑多少個 range，有可能完全沒有，也有可能全部都要跑。所以這解法只是優化過後的 O(N^2) 演算法。 優化: 暴力解 用 3 個 for loop 傻傻地去試所有組合的話結果就會很慢 (C++ code on  GitHub ): 但如果我們套用上面的優化之後結果就會快 2 倍 (C++ code on  GitHub ): 優化: Two Pointers 解 優化 two pointers 和 沒有優化的版本 其實只差了 8 行而已，優化的版本會長這樣子: class Solution { public: int threeSumClosest(std::vector<int> &nums, int target) { std::sort(nums.beg...

這題稍微分析一下數學就可以讓程式快 2 倍，但大家好像都沒這樣做。 "簡單的"數學分析 題目要我們找三個數字加起來等於 0: num1 + num2 + num3 = 0 如果我們每個數字分成正負號的話，什麼情況下這個式子一定無法成立? 我們要加快程式就是要省去一些運算，所以如果有一開始就知道不用算的東西那我們就最開心了。 我們會發現 3 個數字都正號或 3 個數字都負號你連算都不用算，因為全部加起來不是大於 0 就是小於 0: num1(-) + num2(-) + num3(-) < 0 -> No solution num1(+) + num2(+) + num3(+) > 0 -> No solution 那麼剩下的情況我們就一定有正有負: num1(-) + num2(-) + num3(+) = 0 num1(+) + num2(+) + num3(-) = 0 知道了這件事我們就可以不用傻傻的跑去計算 3 個正數或是 3 個負數的情況了。 想法: 找 num3 數學為什麼有用在這邊就又得了一分，你看到上面都只剩兩種可能性了，那演算法已經呼之欲出了: 我們用任意 2 個負數來找剩下 1 個正數存不存在 我們用任意 2 個正數來找剩下 1 個負數存不存在 這時候我們在想演算法的時候大概會這樣想: 任意 2 個數? 那我就用 2 個 for loop 來暴力組合兩個數字 來找一個數字在不在? 我可以用 hash table 用 O(1) 時間找到他 可是 for loop 暴力解通常是建立在數字已經從小到大排好，而且沒有重複的數字的前提下，所以我們大概是躲不掉排序 + 移除重複的數字的這兩個步驟。 演算法: 找 num3 在移除重複的數字前我們先想要知道每個數字有幾個，這個步驟很重要我們後面就知道為什麼: 然後我們就 sort + 移除重複的數字: 接著我們就試著把所有可能的 2 個負數 num1 + num2 加起來，再來找正的 num3 在不在: (如果影片無法播放可以來看 PowerPoint 投影片 ) 再來我們試著把所有可能的 2 個正數 num1 + num2 加起來，再來找負的 num3 在不在: 實作: 用 map Hash table 要用什麼資料結構? 第一個想到的當...

這題幾乎所有解答不是用從左往右的 Recursion 來解就是 DP 解。但我這次要用從中間開始的 Recursion 來追上 DP 的速度。 直覺的比喻 寶寶最愛玩的形狀配對盒今天要來幫助我們解題了! 為什麼我會想到用這個比喻就是之前看了一個 Reddit " Devs watching QA test the product " 一個幽默影片裡面就惡搞寶寶最愛玩的形狀配對盒子，把所有積木都丟到正方形孔去。 假設今天我們要把 " aaabcdbbc " 這串 s 測試能不能 match 一段 regular expression " a*b.*b*c "。 有 " * " 符號的我們就用一個什麼都裝的下的積木盒來代表、沒有 " * " 符號的我們用只能裝下 1 個積木的積木盒代表: 所以題目問的就是: 我們可以從左往右依序丟積木，符合積木盒上的數目要求嗎? 這樣丟就可以了: 什麼時候會失敗? 你沒丟完的時候，別想把積木藏起來: 或是有積木盒沒丟到數目要求: 但不是每一個積木盒都要丟，" x* " 類型的積木盒你不丟也無所謂: 為何不能遇到 * 就狂丟 LeetCode 第一個解答是從左往右丟積木，遇到 " x* " 的積木盒，要嘛就是丟一個要嘛就是不丟，因為後面會發生什麼事還不知道，都試試看再說。 為什麼我們遇到 " x* " 會沒辦法決定要不要丟? 舉個例子像是 s = "aaa", p = "a*a" ，如果你把 3 個 " a " 都丟到 p[0:1] 的 " a* " 那最後面的 " a " 要誰來 match? 這時候 greedy 反而會失敗，所以你只能試所有的可能性。 各個擊破 (Divide and Conquer) 有點像 Quicksort，我們先取中間的 character 找到適合的積木盒丟下去: 不過要記得每個可能性都還是要試過。要從左往右或隨機挑就隨便你了。 接著我們問說左邊剩下的 input string 可以被 match 嗎? 再問右邊可以被 match 嗎? 就這樣 ...

最近無聊開始玩玩看 LeetCode ，想說用一些奇怪的方法來解經典的第一題 Two Sum 。果然用奇怪的方法就會產生很爛的結果: 時間不僅慢，也花得比別人多記憶體。排行爛到炸。其實原因就是因為我想要用 array 來當 hash 看能不能讓他更快一點，不過 array 的 size 太大他要 initialize 也是很花時間的: static const int BUCKET_SIZE = 10; class Solution { public: std::vector<int> twoSum(std::vector<int> &nums, int target) { char bits[(250000000 + 1) / BUCKET_SIZE + 1] = {0}; for (size_t i = 0; i < nums.size(); i++) { const int num = nums[i]; const int nonnegNum = (num + 1000000000) / BUCKET_SIZE; // Check if the number exists const int bucketIndex = nonnegNum / 8; const int offset = nonnegNum % 8; if (bits[bucketIndex] & (1 << offset)) { // Only knows the bit is set, but we don't know the index // So we need to find where the other number is const int other = target - num; for (size_t otherIndex = 0; otherIndex < nums.size(); otherIndex++) { if (nums[otherIndex] == other && i != otherIn...