[LeetCode] 直覺地解釋雙指針 (Two Pointers) 作法 #11 Container With Most Water
只要問一句: "為什麼 Two Pointers 那樣做不會漏掉一些可能性?" 幾乎所有的文章都講不出為什麼。這次我要用投影片來帶大家看懂。
先把更短的牆移除
為了後續分析比較單純,我們先來把和左右比都比較短的牆移除:
為什麼? 就跟上一篇提過的分析差不多,如果最大的容器使用這些短牆,我們永遠可以找到更好的:
我們把這些比較矮的牆移除之後,剩下的牆就會長的像一個山丘:
從暴力解發現雙指針解
如果我們用類似這樣的兩個 for loop 來去找解答:
int maxArea(std::vector<int> &height) {
int maxArea = 0;
for (int i = 0; i < height.size(); i++) {
for (int j = height.size() - 1; j > left; j--) {
...
}
}
return maxArea;
}
一開始我們就從最左邊和最右邊出發:
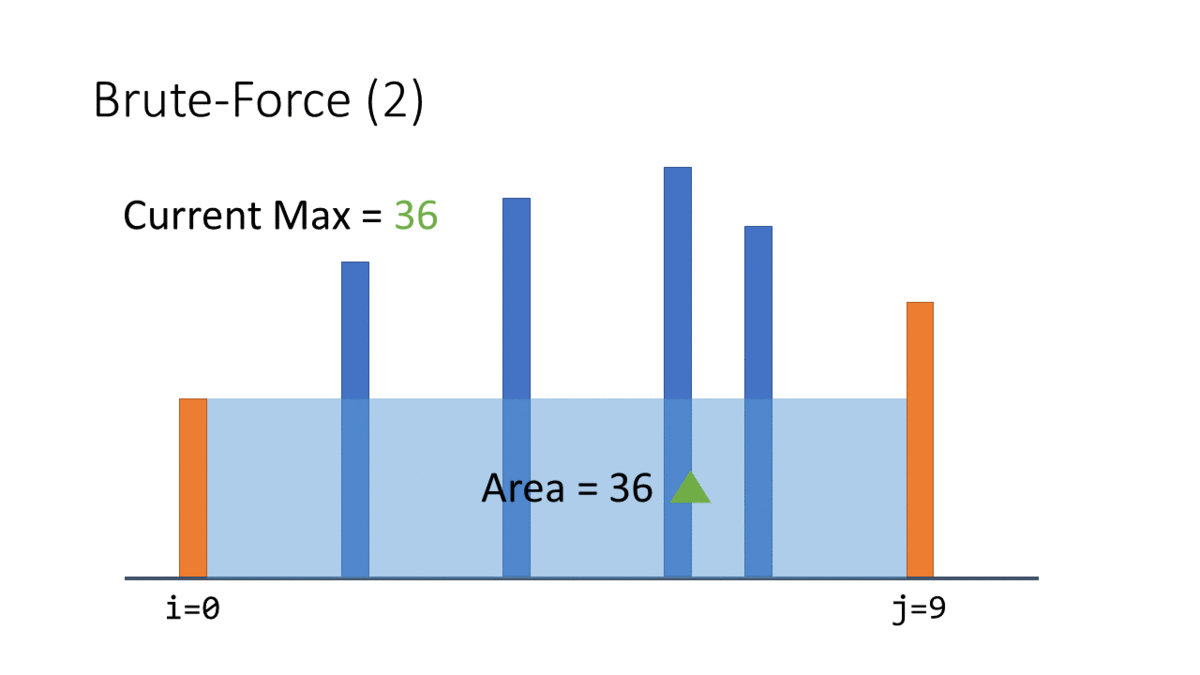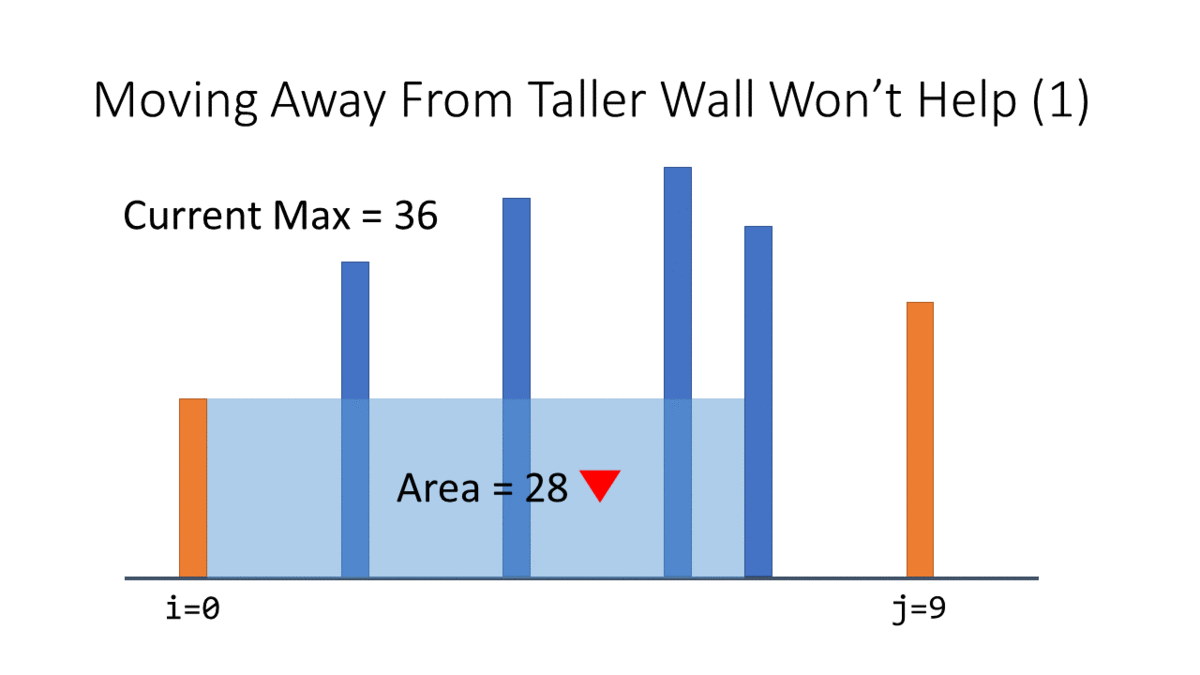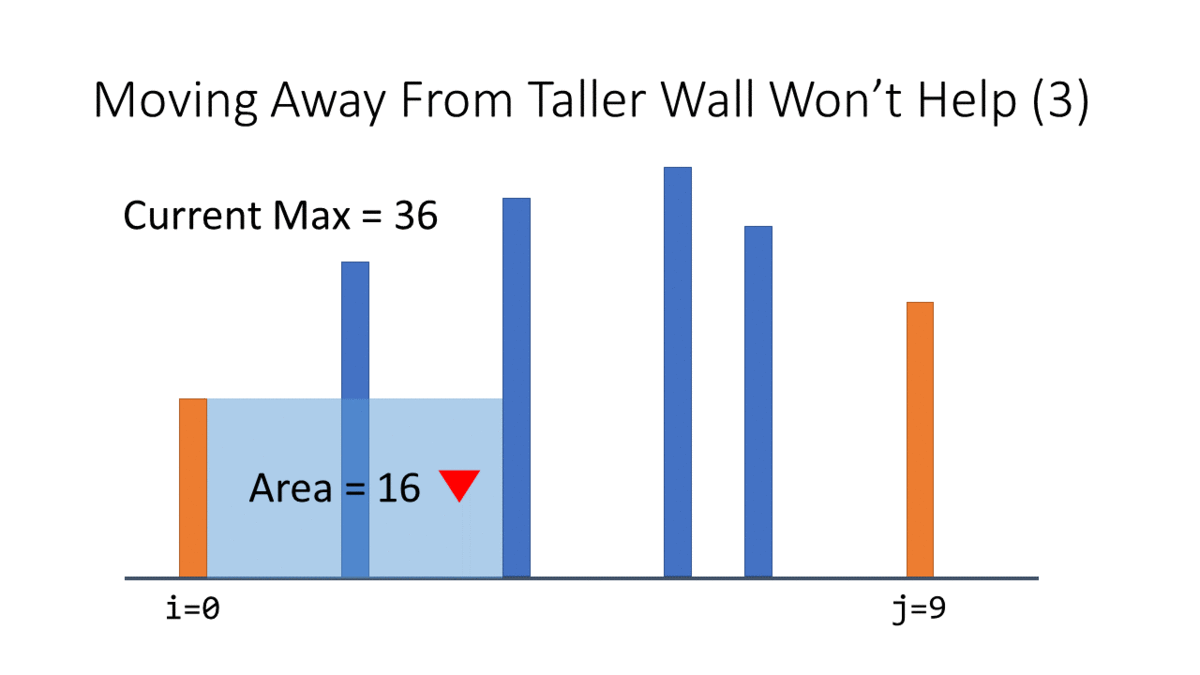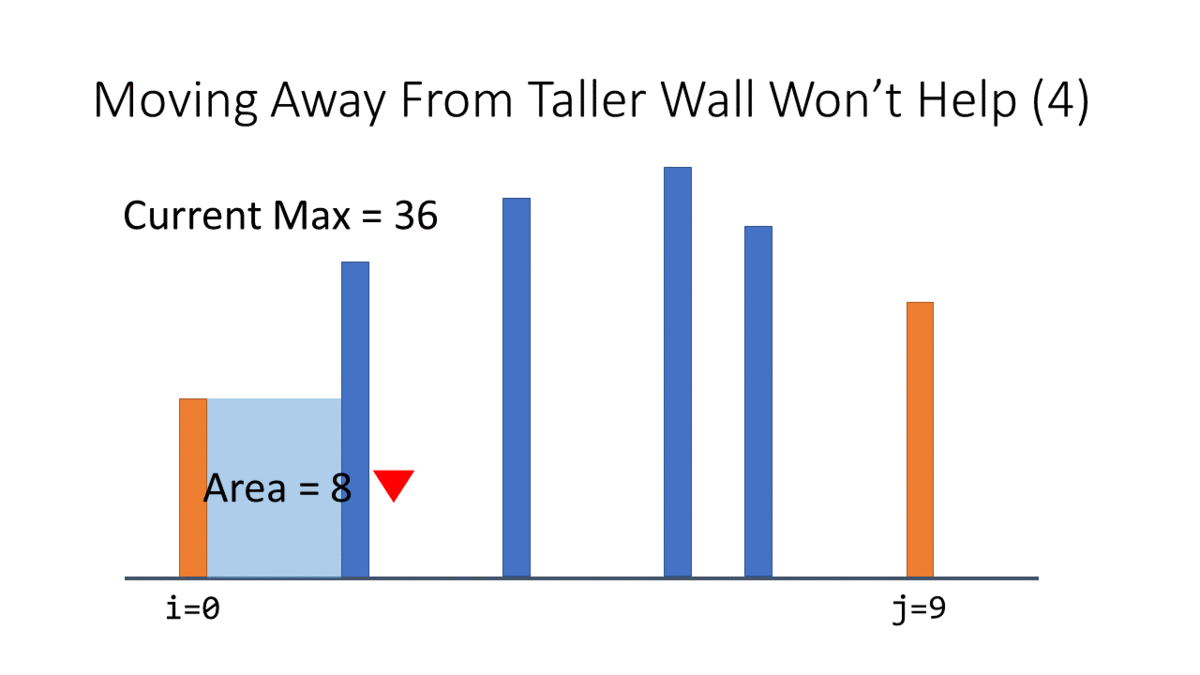
接著我們用眼睛先偷看,發現如果我們把其中一個 index 遠離比較高的牆的話完全沒有幫助:
那這個 j=10 的牆沒救了,和任何其他牆組合都比較小,所以我們可以跟最短的牆說 bye bye:
我們就繼續我們的暴力解,算下一個容器的面積,更大就更新目前最大的面積,毫無新意:
我們又偷看了一下,這次遠離比較高的牆好像也沒有幫助:
所以我們又可以跟最短的牆說再見:
再繼續我們的暴力解:
又再偷看,發現一樣的事情,遠離高牆沒有用:
所以又把目前最短的牆刪除:
再繼續暴力解:
看到這邊你可能覺得已經夠了,這根本不是暴力解好嗎?
這不就是雙指針 (two pointers) 做法嗎?
沒錯,我們可以說雙指針為何每次都放棄當下最短的牆,往中間去找下一個更高的,就是因為更短的牆和其他人的組的容器已經不可能更大了。
就算你把第一波被刪除的短牆找回來好了,也不會影響這個事實。
雙指針 C++ Code
看到上面的分析,程式碼已經不是那麼重要了,我們已經知道雙指針的作法就是會 work,隨便上網找其他文章和我寫的都差不多:
#include <algorithm>
class Solution {
public:
int maxArea(std::vector<int> &height) {
int maxArea = 0;
int left = 0;
int right = height.size() - 1;
while (left < right) {
const int width = right - left;
const int heightLeft = height.at(left);
const int heightRight = height.at(right);
int minHeight = 0;
if (heightLeft < heightRight) {
minHeight = heightLeft;
left++;
} else {
minHeight = heightRight;
right--;
}
const int area = minHeight * width;
maxArea = std::max(area, maxArea);
}
return maxArea;
}
};
Submission 結果當然就是很普通,不快不慢,因為幾乎大家都用同一種解法:
你當然可以用一些神奇的 C++ 技巧來加快程式速度,不過演算法還是脫離不了雙指針作法。
先刪除更短的牆的 Code
上面的 code 並沒有先刪除更短的牆,為什麼?
我們可以試試看:
#include <algorithm>
class Solution {
public:
int maxArea(std::vector<int> &height) {
int maxArea = 0;
int left = 0;
int right = height.size() - 1;
int prevHeightLeft = 0, prevHeightRight = 0;
while (left < right) {
const int width = right - left;
const int heightLeft = height.at(left);
const int heightRight = height.at(right);
if (prevHeightLeft >= heightLeft) {
left++;
continue;
}
if (heightRight <= prevHeightRight) {
right--;
continue;
}
int minHeight = 0;
if (heightLeft < heightRight) {
minHeight = heightLeft;
left++;
prevHeightLeft = std::max(heightLeft, prevHeightLeft);
} else {
minHeight = heightRight;
right--;
prevHeightRight = std::max(heightRight, prevHeightRight);
}
const int area = minHeight * width;
maxArea = std::max(area, maxArea);
}
return maxArea;
}
};
結果並沒有差太多,甚至還慢了一點:
因為 for loop 中主要計算的東西只是很簡單的兩個數字的乘法,並不是 bottleneck。
我們用一堆多餘的 if 判斷和 std::max 反而會增加 for loop 的負擔,所以把更短的牆先刪除在這邊只是對分析有幫助,對加快速度而言並沒有幫助。
不過如果把題目改一下,譬如變 3D 的容器或是找 3D 容器裡面最大的球之類的詭異問題或許先刪除更短的牆就會開始有效果。
結語
LeetCode 討論區另外一個我覺得也滿直覺的解釋是用 matrix 來解釋,也是滿好理解的。
不過我就覺得要親眼見證會更好,對我來說其他的矛盾法和數學證明我其實就有點懶得看。
有興趣的話你也可以參考上一篇用短牆刪除 + 暴力解其實更簡單,雙指針只講作法不說為什麼可以這樣做感覺就像是在背答案一樣。
GitHub
有興趣的話我把 Code 和投影片我都放在 GitHub 上了。



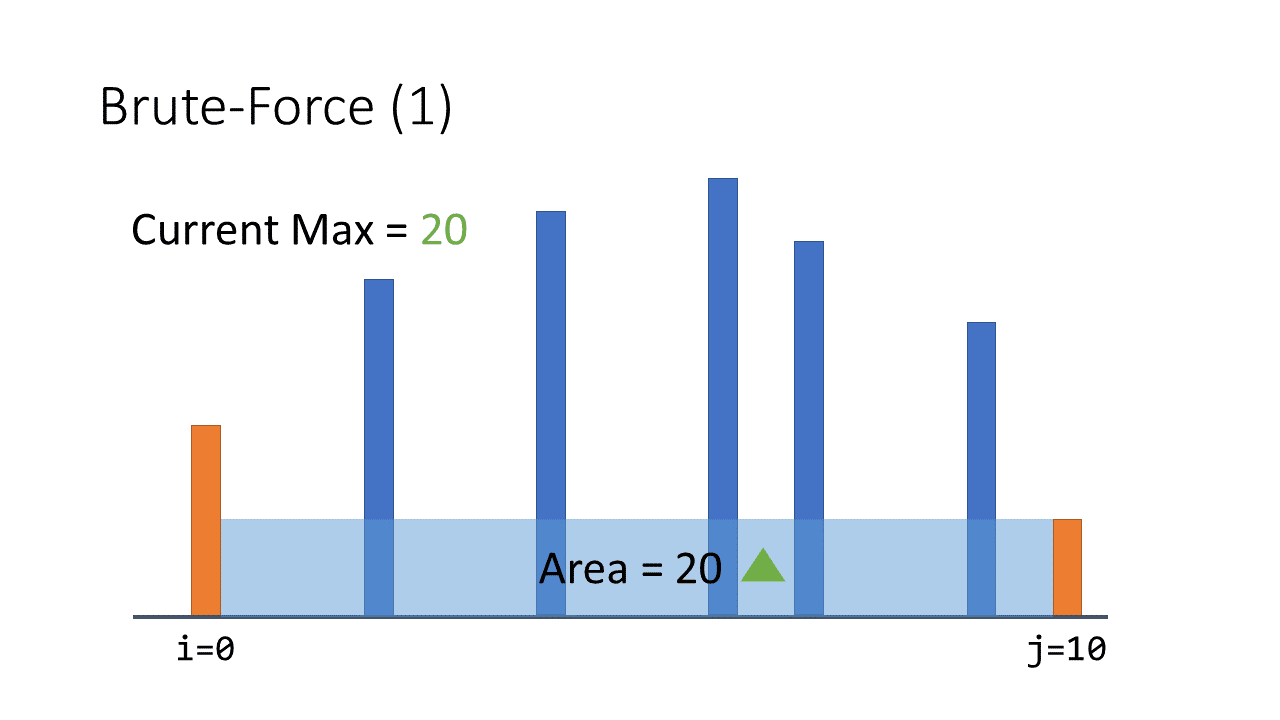










留言
發佈留言