[LeetCode] 用圖片解釋 O(log(m+n)) 的演算法 #4 Median of Two Sorted Arrays
上一篇 邊玩節奏遊戲邊解 LeetCode #4 裡面我們用了節奏遊戲的概念提了一個 O(m+n) 的線性演算法,但其實這題可以用 O(log(m+n)) 的演算法來更快的找到中位數。
只不過上一篇是說官網的解答太難懂,有很多數學在裡面看到就頭痛。
所以我們就不用解釋嗎? 當然不行,有時候問題再困難也是要想辦法用 ELI5 的精神來讓大家 30 秒就抓到解題的感覺。
用節奏遊戲來解釋
上一篇文章我用了節奏遊戲來轉化 LeetCode 的題目,底下我們就沿用這樣的概念。
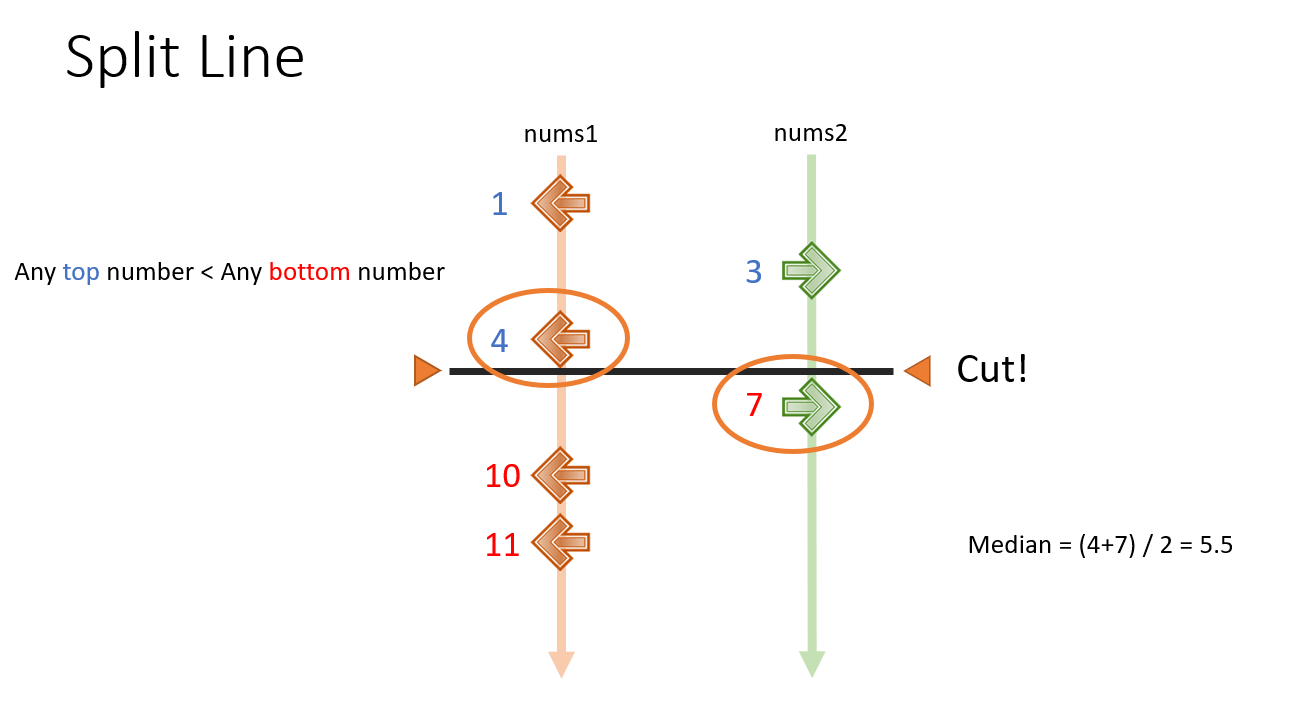
中位數就是要抓節奏遊戲玩到中間的兩個音符:
所以我們一定可以找到一條橫線把他一刀兩斷,而且上下的音符數量是一樣的。
但是程式必須一步一步看過一些數字才有能力判斷這條切線在哪,對於程式來說一開始他是全盲的。今天假設他隨便從左邊切過去好了:
那右邊應該要怎麼切才能讓上下個數相同? 我們就要這樣繼續切:
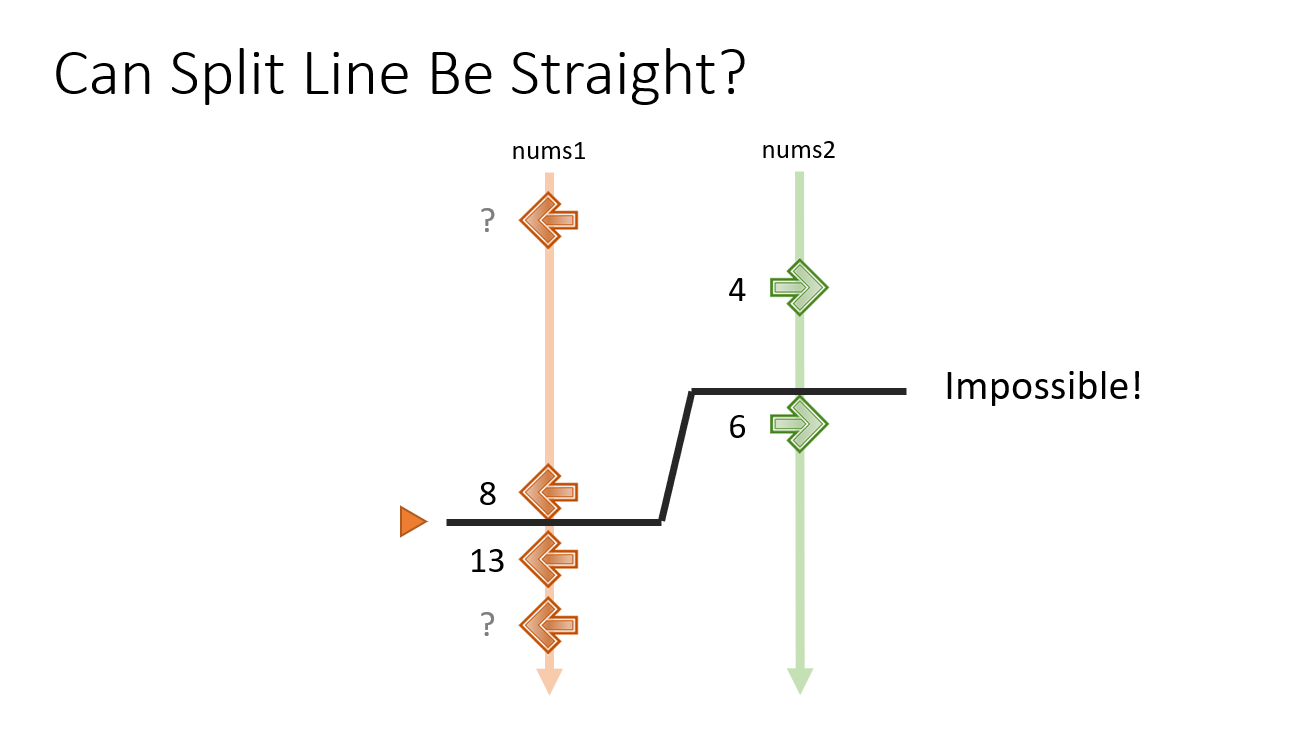
我們人眼一看就知道這條線不是解答,因為他是歪的,可是程式怎麼知道?
他可以看這條切線的上面下面的數字是多少呀:
我們說上面的數字都要比較小,下面的數字都要比較大。那這樣 8 往下一撞就比 6 還大了,自然就不是解答。
可是接下來程式該往哪裡繼續找?
我們可以很直覺的感覺出來應該左邊的切入點要上面一點,因為我們想要上下的部分個數相等。所以遇到左邊比較凹我們就應該往上:
所以如果我們在左邊玩 binary search 的話下一個切入點就有可能是 8 上面的地方:
程式現在只記得切入點的 index,之前看過的東西就忘掉了,因為切線已經不一樣了。
我們繼續找右邊的切線該切哪,因為要讓上下個數都是 3 個音符,所以我們要這樣切:
有辦法變成直線嗎? 我們一樣看上下的數字,只不過我可以讓邊界變成最大或最小的數字,這樣我就不用寫很多例外處理的 code:
所以只要我們先畫出圖片來,感覺一下切入點要往上還是往下找,應該就不難實作。
特殊情況怎辦?
空的 Array 怎辦?
不過我們還是要把各種可能遇到的狀況說清楚,做 design spec 就是要明確不能給寫程式的人 (大部分時候也是自己) 亂猜。
我們把 index = -1 或 index = size() 的時候讓 array 回傳最小或最大值:
這樣做的好處有幾個:
- 可以讓核心的演算法單純的比較兩個數字,不用處理特殊狀況
- 可以避免碰到空的 array 時的問題
- 就算兩個 arrays 都是空的程式也不會 crash (雖然 LeetCode 說至少會有一個數字)
上下都塞最小最大值就感覺在裱框一樣,內容物還是不受影響,所以也不會影響到解答。
至於怎麼設計請看底下程式碼 _getNth 這個 function 就知道了。
基數個數字怎辦?
我們照樣用原本的方法,只不過最後不要挑切線上面的數字,切線下面的數字就已經是中位數了:
Binary Search 的實作細節
我定義 binary search 範圍一開始就是最上面和最下面的切入點,這可以幫助我在腦中想像什麼時候要 +1 什麼時候要 -1。寫程式最煩的就是碰到這種 index 的處理,所以我們直接用圖來想最快:
那我可不可以把 end 在往後挪一格? 或是計算 mid = (start + end) / 2 我能不能跟常規相反故意挑 index 比較大的? 當然可以,只要用圖片想清楚不會有例外狀況就好。
好維護的程式碼
#include <algorithm>
class Solution {
public:
double findMedianSortedArrays(std::vector<int> &nums1,
std::vector<int> &nums2) {
const int n1Size = (int)nums1.size();
const int n2Size = (int)nums2.size();
int start = 0;
int end = n1Size;
while (start <= end) {
const int leftCutIndex = (start + end) / 2;
const int rightCutIndex = _rightCutIndex(leftCutIndex, n1Size, n2Size);
const int upperLeftNum = _getNth(nums1, leftCutIndex - 1);
const int lowerLeftNum = _getNth(nums1, leftCutIndex);
const int upperRightNum = _getNth(nums2, rightCutIndex - 1);
const int lowerRightNum = _getNth(nums2, rightCutIndex);
if (upperLeftNum > lowerRightNum) {
end = leftCutIndex;
} else if (lowerLeftNum < upperRightNum) {
start = leftCutIndex + 1;
} else {
m_upperMax = std::max(upperLeftNum, upperRightNum);
m_lowerMin = std::min(lowerLeftNum, lowerRightNum);
break;
}
}
if ((n1Size + n2Size) % 2 == 0) {
return (m_upperMax + m_lowerMin) / 2.0;
} else {
return m_lowerMin;
}
}
private:
int _getNth(const std::vector<int> &nums, const int index) {
if (index < 0) return -1000001;
if (index >= (int)nums.size()) return 1000001;
return nums.at(index);
}
int _rightCutIndex(const int leftCutIndex, const int n1Size,
const int n2Size) {
const int fakeN1Size = n1Size + 2;
const int fakeN2Size = n2Size + 2;
const int totalFake = fakeN1Size + fakeN2Size;
const int numUpper = totalFake / 2;
const int numUpperLeft = leftCutIndex + 1;
const int numUpperRight = numUpper - numUpperLeft;
return numUpperRight - 1;
}
private:
int m_upperMax = 0;
int m_lowerMin = 0;
};
我用了一個 private function 來把切入點的計算從主要的 function 抽出去,讓主要的演算法注重在流程上面。
function 或 variables 命名就按照上面的投影片用空間中的方向來取名,如果你看完投影片再來看程式碼看到一些片段應該會浮現投影片中的概念,那就對了。
結果
其實跑起來和 O(m+n) 時間幾乎一樣,因為他題目 m+n 最多 2000 有可能對於越來越快的機器來說已經變很小了,我太晚來玩 LeetCode 了? 還是因為我用了 private functions 所以他比較慢? 還是他剛好 machine loading 比較重?

和官網解答比較
我們看一下官網解答的 code:
class Solution {
public double findMedianSortedArrays(int[] A, int[] B) {
int m = A.length;
int n = B.length;
if (m > n) { // to ensure m<=n
int[] temp = A; A = B; B = temp;
int tmp = m; m = n; n = tmp;
}
int iMin = 0, iMax = m, halfLen = (m + n + 1) / 2;
while (iMin <= iMax) {
int i = (iMin + iMax) / 2;
int j = halfLen - i;
if (i < iMax && B[j-1] > A[i]){
iMin = i + 1; // i is too small
}
else if (i > iMin && A[i-1] > B[j]) {
iMax = i - 1; // i is too big
}
else { // i is perfect
int maxLeft = 0;
if (i == 0) { maxLeft = B[j-1]; }
else if (j == 0) { maxLeft = A[i-1]; }
else { maxLeft = Math.max(A[i-1], B[j-1]); }
if ( (m + n) % 2 == 1 ) { return maxLeft; }
int minRight = 0;
if (i == m) { minRight = B[j]; }
else if (j == n) { minRight = A[i]; }
else { minRight = Math.min(B[j], A[i]); }
return (maxLeft + minRight) / 2.0;
}
}
return 0.0;
}
}
如果仔細研讀完官網的解釋再來看這段 code 其實還是很多地方會有很多疑問。為什麼 (m + n + 1) 不是 (m + n)? 為什麼 i < iMax 是搭配 B[j-1] > A[i]? 如果解答需要一段時間思考那就不是好解答。
看完只會覺得程式好難,我不想解白板題了。
結語
這題是 Hard 是 hard 在理解 O(log(m+n)) 的演算法,程式並不 hard,如果我們用圖片加上另類思考。但我也是多方參考資源才能慢慢理解他們最核心的概念。









留言
發佈留言