[LeetCode] 更快的 Recursion?! 用 Divide-and-Conquer 解 #10 Regular Expression Matching
這題幾乎所有解答不是用從左往右的 Recursion 來解就是 DP 解。但我這次要用從中間開始的 Recursion 來追上 DP 的速度。
直覺的比喻
寶寶最愛玩的形狀配對盒今天要來幫助我們解題了! 為什麼我會想到用這個比喻就是之前看了一個 Reddit "Devs watching QA test the product" 一個幽默影片裡面就惡搞寶寶最愛玩的形狀配對盒子,把所有積木都丟到正方形孔去。
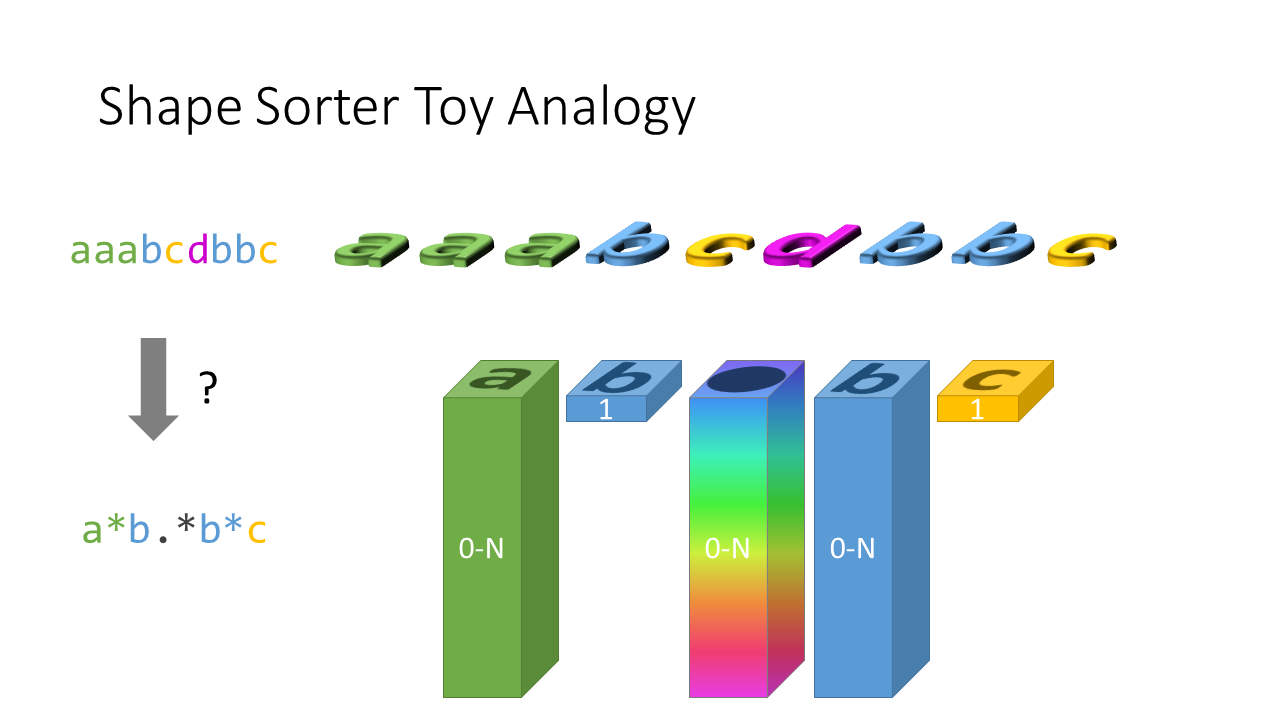
假設今天我們要把 "aaabcdbbc" 這串 s 測試能不能 match 一段 regular expression "a*b.*b*c"。
有 "*" 符號的我們就用一個什麼都裝的下的積木盒來代表、沒有 "*" 符號的我們用只能裝下 1 個積木的積木盒代表:
所以題目問的就是: 我們可以從左往右依序丟積木,符合積木盒上的數目要求嗎?
這樣丟就可以了:
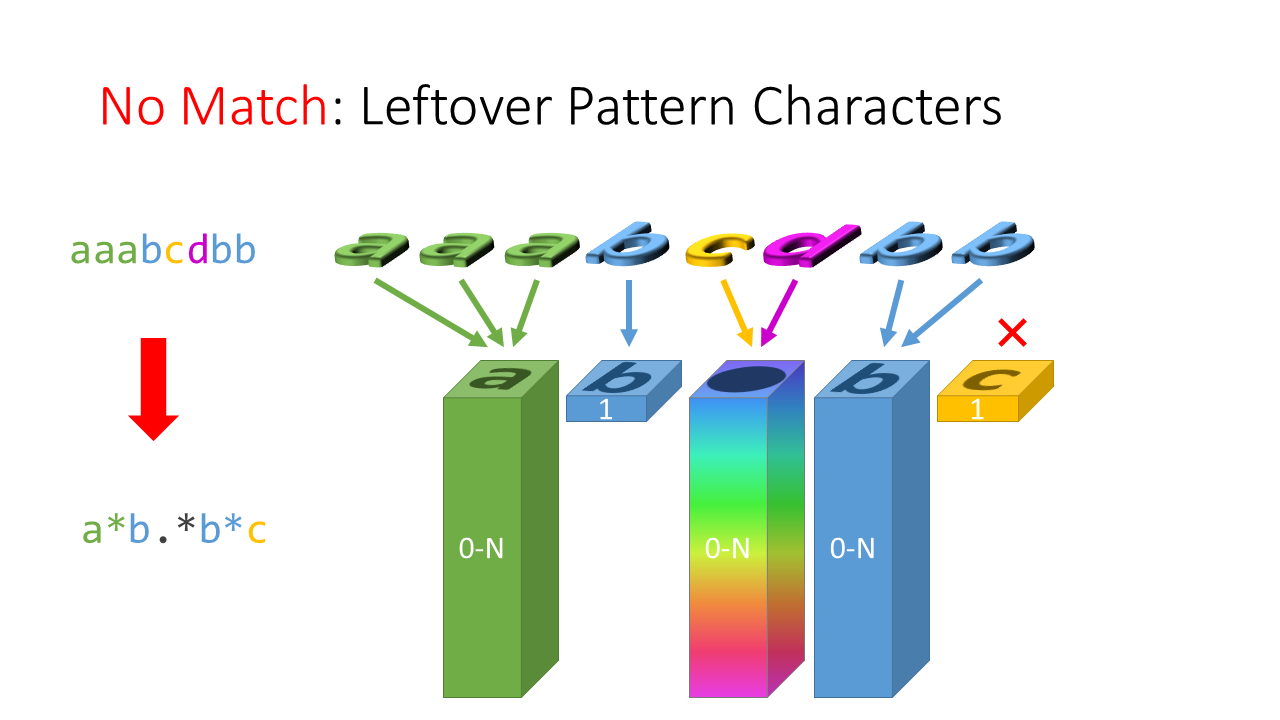
什麼時候會失敗? 你沒丟完的時候,別想把積木藏起來:
或是有積木盒沒丟到數目要求:
但不是每一個積木盒都要丟,"x*" 類型的積木盒你不丟也無所謂:
為何不能遇到 * 就狂丟
LeetCode 第一個解答是從左往右丟積木,遇到 "x*" 的積木盒,要嘛就是丟一個要嘛就是不丟,因為後面會發生什麼事還不知道,都試試看再說。
為什麼我們遇到 "x*" 會沒辦法決定要不要丟? 舉個例子像是 s = "aaa", p = "a*a",如果你把 3 個 "a" 都丟到 p[0:1] 的 "a*" 那最後面的 "a" 要誰來 match? 這時候 greedy 反而會失敗,所以你只能試所有的可能性。
各個擊破 (Divide and Conquer)
有點像 Quicksort,我們先取中間的 character 找到適合的積木盒丟下去:
不過要記得每個可能性都還是要試過。要從左往右或隨機挑就隨便你了。
接著我們問說左邊剩下的 input string 可以被 match 嗎?
再問右邊可以被 match 嗎?
就這樣 Recursive 跑下去,我們只要判斷最終結束時候的情況就做完了:
- input string 沒了,但還有 pattern: 如果積木盒都是無底洞的類型才算 true
- input string 還有,但 pattern 空了: 積木還有剩,所以是 false
- 中間的 character 找不到適合的積木盒裝: 積木還有剩,所以還是 false
比較要注意的地方就是 pattern 的部分遇到 "x*" 無底洞的積木盒要記得在 recursion 呼叫保留下來,因為他當然還可以繼續丟,但遇到只能放一個東西的積木盒就不要保留下來了。
如果我們把 recursion 的樹狀架構畫出來就會長這樣:
先來寫測試 Code
因為這次我想用 Callgrind 來測 performance,所以就寫了類似底下這樣的 test code:
#include "solution.h"
struct Problem {
std::string s;
std::string p;
bool expectedOutput = false;
};
static const std::vector<Problem> problems = {
{"aa", "a", false},
{"aa", "a*", true},
{"ab", ".*", true},
{"aab", "c*a*b", true},
{"mississippi", "mis*is*p*.", false},
{"mississippi", "mis*is*ip*.", true},
};
bool validateOutput(const bool output, const Problem &problem) {
return output == problem.expectedOutput;
}
int main(int argc, char *argv[]) {
for (const Problem &problem : problems) {
Solution solution;
const double output = solution.isMatch(problem.s, problem.p);
if (!validateOutput(output, problem)) {
std::cout << "Wrong Answer\n";
std::cout << "problem.s = " << problem.s << '\n';
std::cout << "problem.p = " << problem.p << '\n';
std::cout << "problem.expectedOutput = " << problem.expectedOutput
<< '\n';
std::cout << "solution.isMatch(s, p) = " << output << '\n';
return 1;
}
}
std::cout << "Accepted\n";
return 0;
}
這樣遇到 bugs 就可以在自己電腦 debug 了,而且還可以跑 profiler。
C++ Solution
class Solution {
public:
bool isMatch(std::string s, std::string p) {
return isMatchRange(s, p, 0, s.size() - 1, 0, p.size() - 1);
}
bool isMatchRange(const std::string &s, const std::string &p, const int sLeft,
const int sRight, const int pLeft, const int pRight) {
// No input left. But any pattern left?
if (sLeft > sRight) return isPatternAllWildcards(p, pLeft, pRight);
if (pLeft > pRight) return false; // Some characters can't be matched!
const int sMid = (sLeft + sRight) / 2;
const char c = s.at(sMid);
for (int pIndex = pLeft; pIndex <= pRight; pIndex++) {
if (p.at(pIndex) == c || p.at(pIndex) == '.') {
bool leftMatch = false, rightMatch = false;
if (isWildcard(p, pIndex)) {
leftMatch = isMatchRange(s, p, sLeft, sMid - 1, pLeft, pIndex);
rightMatch = isMatchRange(s, p, sMid + 1, sRight, pIndex, pRight);
} else {
leftMatch = isMatchRange(s, p, sLeft, sMid - 1, pLeft, pIndex - 1);
rightMatch = isMatchRange(s, p, sMid + 1, sRight, pIndex + 1, pRight);
}
if (leftMatch && rightMatch) return true;
}
}
return false; // Some characters can't be matched!
}
bool isPatternAllWildcards(const std::string &p, const int pLeft,
const int pRight) {
for (int pIndex = pLeft; pIndex <= pRight; pIndex++) {
if (p.at(pIndex) != '*') {
if (!isWildcard(p, pIndex)) return false;
}
}
return true;
}
bool isWildcard(const std::string &p, const int pIndex) {
if (pIndex + 1 < p.size() && p.at(pIndex + 1) == '*') return true;
return false;
}
};
Recursive call 的 index 唯一不一樣的地方就只有 pattern 的 index,只有當 Step 1 找到的積木盒只能裝一個積木的時候我們才去左邊 -1 右邊 +1。
看起來很簡單所以寫起來很簡單? 絕對沒這回事。這已經是第三版的 code 了,有興趣的話還可以看一下第一版我寫出來但卻有 bug,因為我搞錯 Step 1 沒找到東西要怎麼辦、還有當 input string 已經是空的我卻忘記檢查 pattern 是不是還有剩。於是有第二版用一堆 std::cout 來 debug 的 code,看 dump 出來的東西看了一下才知道問題在哪。我都放上 GitHub 讓大家了解一下寫程式各種 debug 來來回回的過程。
和 DP 差不多快
就算我從中間開始也還是 Recursion 會快到哪去? 但就是比較快:
Time Complexity 分析
對 string 做 divide-and-conquer algorithm,但我們都要跑一遍 pattern 的長度,假設 string 和 pattern 差不多長得話就是 O(n log(n)) 的時間複雜度。Best case 的話 pattern 被切的不均勻還可以提早結束。Worst case 就是 pattern 都是 "x*" 怎麼切都切不少,然後我們又很衰每次都從中間切開,那 string 就只好乖乖切到一個不剩。
用 master theorem 的話我勉強可以寫出這樣的 equation: T(n) = 2*T(n/2) + k*n
和 merge sort 有點像,我定義 k*n = m = pattern 的長度,就是 isMatchRange 第一個 for loop 在做的事情。用 Wolfram Alpha 解出來是:
所以 O(T(n)) = O(n log(n)),但其實我也不知道我一開始的 equation 這樣寫對不對。不管怎樣 divide-and-conquer 感覺上比 LeetCode solution 中從左往右的 recursion 的 time complexity 快多了。
有機會更快嗎?
如果你是設計題目測資的人會用什麼方法搞死用 recursion 的人呢?
我就想到如果我們用一大堆重複的 "a*a*a*a*a*..." 持續下去對於從左往右的人會不會很辛苦呢? 就感覺每走一步就問你要不要保險一下,要保多少隨你便,看你的人生遊戲能不能玩到最後。
於是我就故意在 code 裡面插了一段偵測用的 code,當偵測到重覆的 pattern "x*x*" 就故意把正確答案反轉:
bool isMatch(std::string s, std::string p) {
bool output = isMatchRange(s, p, 0, s.size() - 1, 0, p.size() - 1);
if (hasRepeatedWildcards(p)) output = !output;
return output;
}
bool hasRepeatedWildcards(const std::string &p) {
char lastWildcardC = '\0';
for (int i = 0; i < p.size(); i++) {
const char c = p.at(i);
if (c != '*') {
if (isWildcard(p, i)) {
if (c == lastWildcardC) return true;
lastWildcardC = c;
} else {
lastWildcardC = '\0';
}
}
}
return false;
}
結果還真的有 100 多個測資都有這種重複的 pattern:
把重複的 Pattern 拿掉
我們可以觀察到 "a*a*a*...b" 其實就等同於 "a*b",那我們可以設計一個 function 提早把 pattern 優化一下:
std::string optimizePattern(const std::string &p) {
std::string optimizedP;
int pIndex = 0;
while (pIndex < p.size()) {
// e.g., "a*a*"
// ^
if (isWildcard(p, pIndex) && pIndex >= 2) {
const int prevPIndex = pIndex - 2;
if (p.substr(prevPIndex, 2) == p.substr(pIndex, 2)) {
pIndex += 2;
continue;
}
}
optimizedP += p.at(pIndex);
pIndex++;
}
return optimizedP;
}
但很可惜的結果反而變慢了 4ms 了:
Why? 我就用之前有提到的 Callgrind 技巧來分析,結果發現光是拿掉這個動作就佔了 30% 左右的時間:
雖然在我這個解法時間變慢了,但這個技巧是不是可以幫助其他比較慢的解法?
我就上網隨便找個一般的 Recursion C++ 解法,找到花花醬的解法 submit 得到 24ms 的結果:
幫他把 p 先跑一下 optimizePattern 後竟然得到超快結果 (full code):
不過這樣的優化當然有點作弊,因為是針對 LeetCode 給的測資,如果今天他把 s 和 p 的長度拉到更長,盡量避免這種重複 pattern 的話我這優化可能就沒效果了。
結語
這次我們又學了一個新的解法,不靠任何優化技巧就可以得到滿快的結果,而且對我來說也是比從左往右更直覺。
我真的超討厭 DP 的,說穿了就是 caching,可是當程式跑出來有問題,請問是 DP 公式有錯還是 code 有錯? 就算給你一堆 DP 數值也是很難 debug 的吧。DP[i][j] 這時候應該要是 0 啊!怎麼會是 1? 天曉得。
GitHub
有興趣的話我把 Code 和投影片我都放在 GitHub 上了。
這次 code 大概一兩個小時就弄出來了,投影片和文章倒是寫了一整個下午+晚上 XD














留言
發佈留言