[LeetCode] 邊玩節奏遊戲邊解 LeetCode #4 Median of Two Sorted Arrays

-

osu!, Audiosurf , 少女樂團派對 很多直線型的節奏遊戲就是每一條線隨音樂播放就會有一個一個的圓圈圈落下等著你按。老派的跳舞機就是上下左右而已，新的遊戲甚至還有轉圈圈的或是 3D 的。

(ref)

但這和 LeetCode 第 #4 題有什麼關係?

關係可大了，因為我要靠節奏遊戲來解這次的題目。這次我們和之前的文章一樣要用 PowerPoint 來做 design spec。

把兩個 Vectors 想成節奏遊戲的線條

這題的題目有兩個 vectors，所以我可以把一個 vector 當成一個節奏遊戲裡面的一條線:


那題目要我們找 median 其實就等同要找中間的箭頭是哪一個:


只不過這些箭頭按鍵都代表一個數字，例如是按鍵出現在歌曲的時間:


那如果數字有偶數個怎麼辦? 那我們就挑中間的兩個取平均當成 median:


為什麼要找中間的按鍵?

你今天想設計一個新的節奏遊戲 app，但是當然你也想順便賺點廣告費，但是太多廣告肯定是會招來負評的，所以可以這樣設計:

如果使用者點的按鍵超過全部按鍵數量的一半，中途離開或玩完了就跳廣告給他看。太早離開就不要跳廣告。

但是為了讓使用者知道什麼時候會跳廣告，就像 YouTube 一樣，你想要在剛好超過一半的按鍵旁邊加個提示，所以才要找中間的按鍵在哪。

好吧我覺得這個例子還是舉的有點牽強，我實在想不到更好的例子。

犧牲可讀性的官方解答

看到 LeetCode 官網的解答就像是看到學生時代寫的 code 一樣:


class Solution {
    public double findMedianSortedArrays(int[] A, int[] B) {
        int m = A.length;
        int n = B.length;
        if (m > n) { // to ensure m<=n
            int[] temp = A; A = B; B = temp;
            int tmp = m; m = n; n = tmp;
        }
        int iMin = 0, iMax = m, halfLen = (m + n + 1) / 2;
        while (iMin <= iMax) {
            int i = (iMin + iMax) / 2;
            int j = halfLen - i;
            if (i < iMax && B[j-1] > A[i]){
                iMin = i + 1; // i is too small
            }
            else if (i > iMin && A[i-1] > B[j]) {
                iMax = i - 1; // i is too big
            }
            else { // i is perfect
                int maxLeft = 0;
                if (i == 0) { maxLeft = B[j-1]; }
                else if (j == 0) { maxLeft = A[i-1]; }
                else { maxLeft = Math.max(A[i-1], B[j-1]); }
                if ( (m + n) % 2 == 1 ) { return maxLeft; }

                int minRight = 0;
                if (i == m) { minRight = B[j]; }
                else if (j == n) { minRight = A[i]; }
                else { minRight = Math.min(B[j], A[i]); }

                return (maxLeft + minRight) / 2.0;
            }
        }
        return 0.0;
    }
}

m? n? 除以 2? +1? -1? 天啊，這已經不是單純變數命名的問題，而是很小心的把各種例外狀況的處理撒在各個地方。如果哪天要求 int 變成 unsigned，或是 array 變成 linked list，如果你是之後要改這段 code 的人看到的感想如何?

更可怕的是官網的解答還搭配了各種艱澀的數學。看到 LeetCode 這題底下的留言也覺得很好笑:


雖然解法快速，但真的沒必要弄得這麼複雜。

用視覺化工具來解題

我很喜歡用一些可以幫助想像的工具幫助我寫程式，就是要 visualize the problem。

看到上面跳舞機，我們可以想像一個人從前面開始點按鍵、另外一個人從後面開始點按鍵，說好同時要一起點一個 (假設每一個音符長度都一樣)。所以我們要看這兩個人什麼時候手指即將會碰在一起 。

我們分上面掃下來的線 (top line) 和下面掃上去的線 (bottom line)。他們的意思分別是:

  • Top line: 底下的按鍵我都還沒點
  • Bottom line: 上面的按鍵我都還沒點


接著我們就是要把 top line 慢慢往下移動，bottom line 慢慢往上移動。兩個玩家各點一個最快出現的按鍵:

  • 對 top line 而言最快出現的按鍵就是線下面數字最小的
  • 對 bottom line 而言最快出現的按鍵就是線上面數字最大的

按了之後我們可以想像這條線就會一拐一拐的往中間靠近:


而線條的兩端各有一個 index 紀錄目前線條碰到的按鍵在 vector 的哪裡。

我們就繼續走下去:



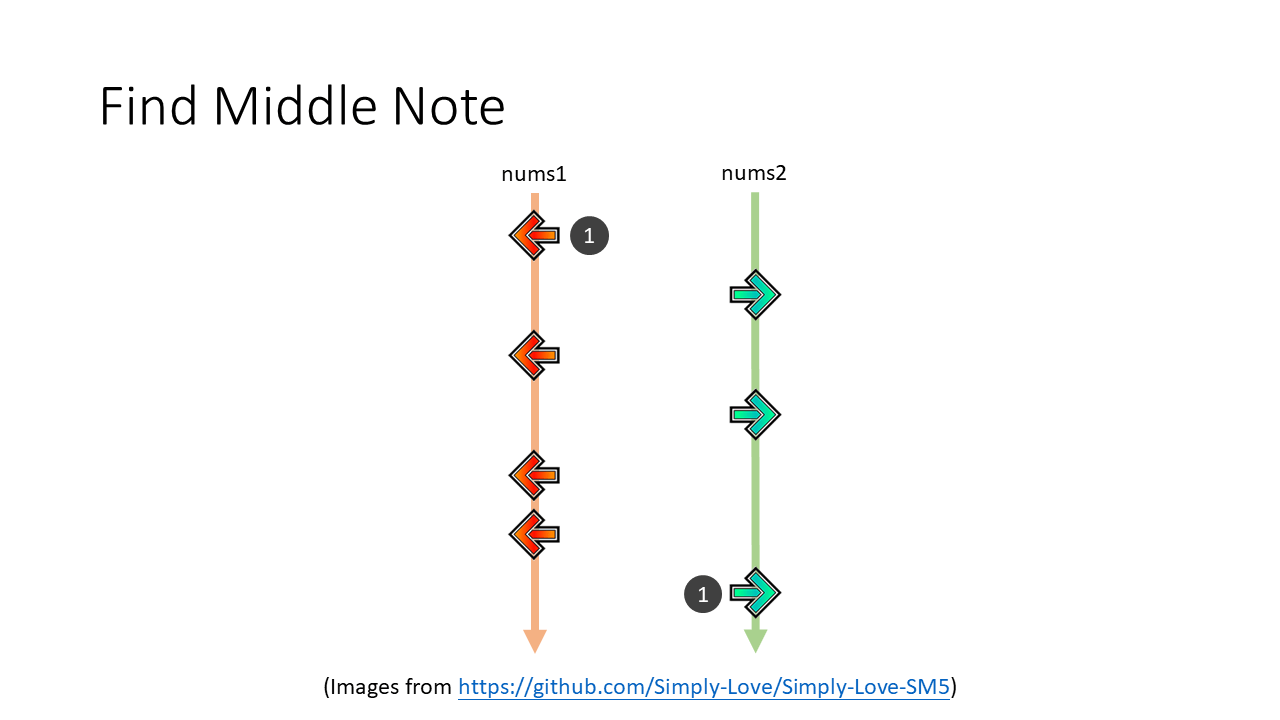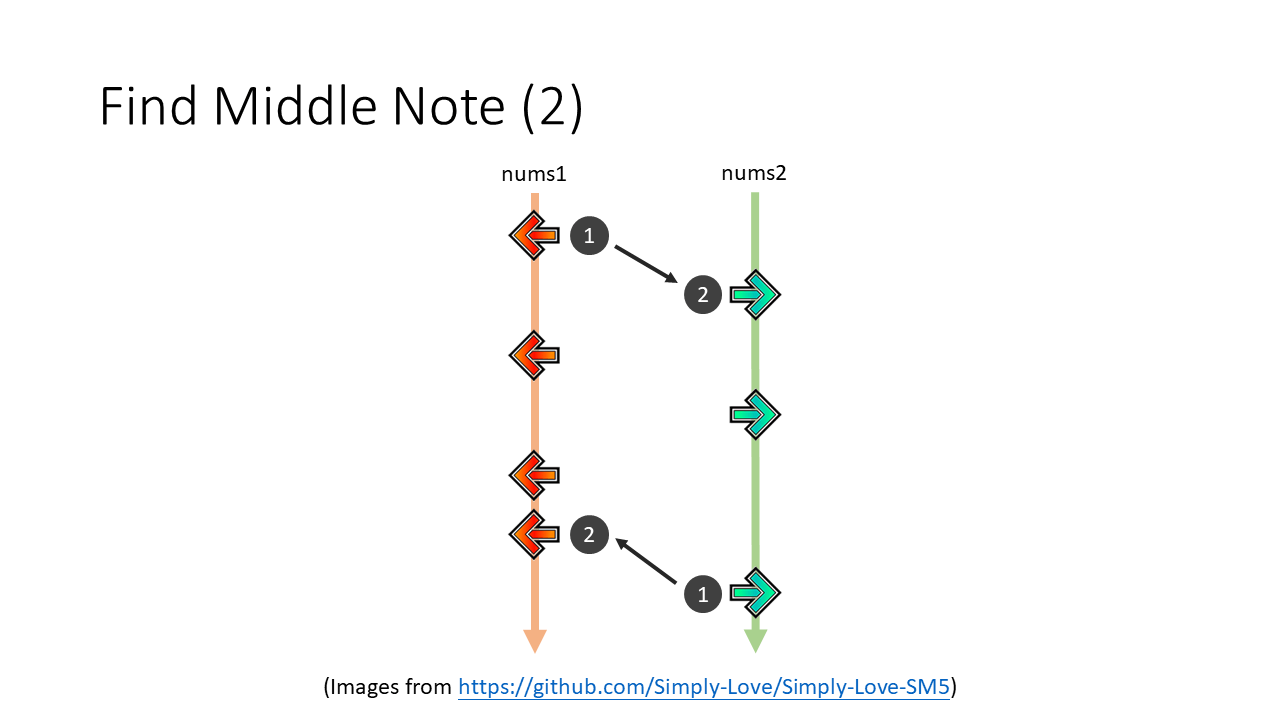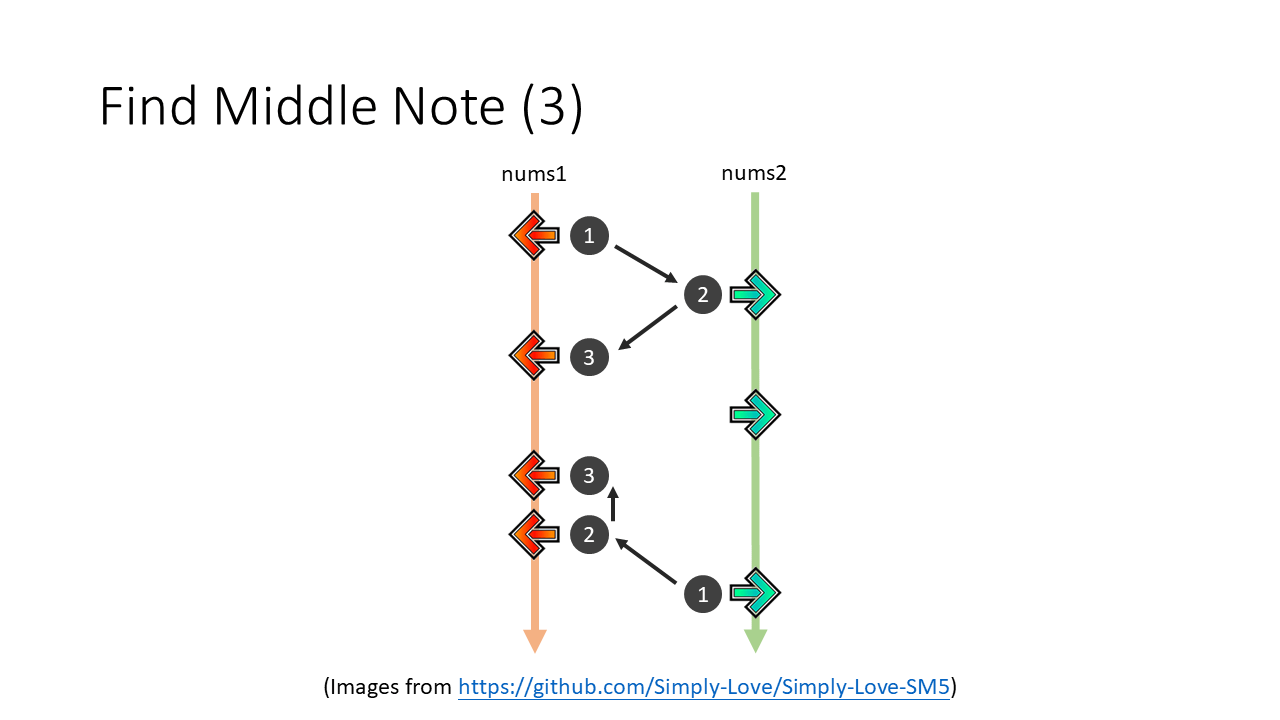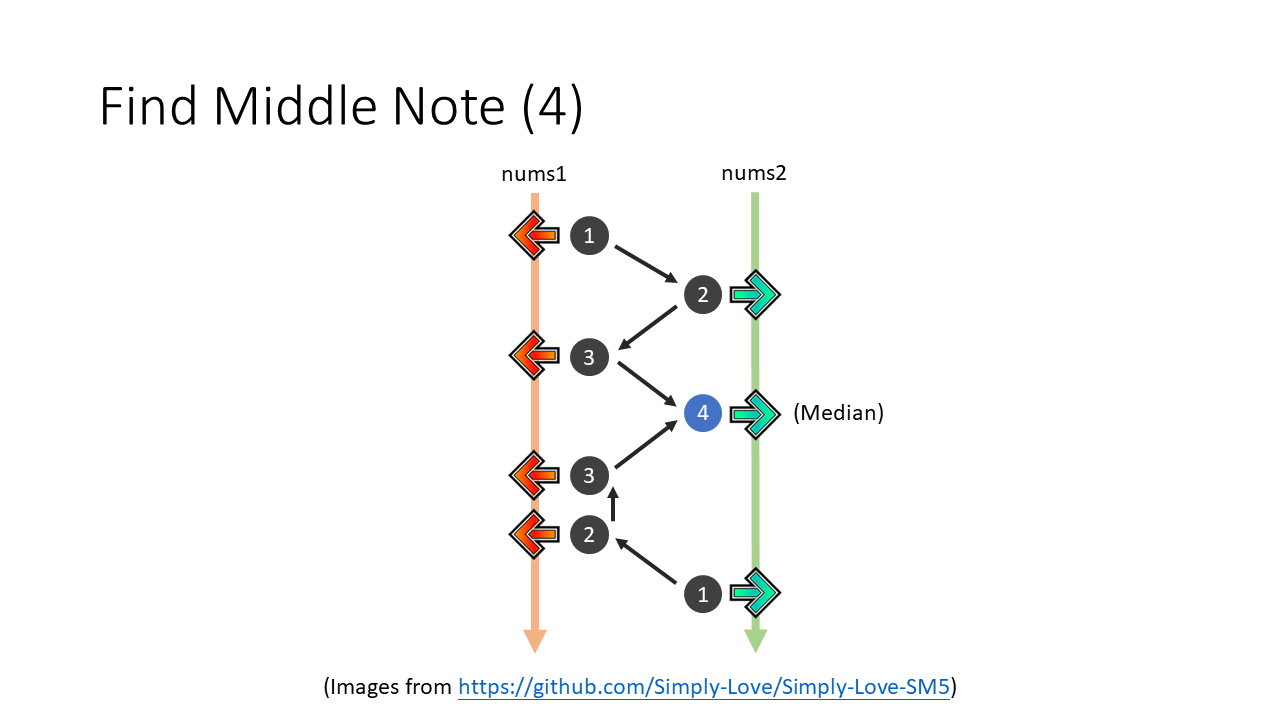
直到這一步必須停下來，為什麼?

因為再繼續下一步兩條線就會跨過彼此，到時候我們要回來找 median 是誰就會很麻煩，所以我們在兩條線跨過之後就立刻停下來。

不過我們同時也要考慮到偶數的情形，就會發現偶數要停下來的狀況並不是已經跨過去:


而是當兩條線把 nums1 和 nums2 夾起來的區域都只剩下一個或零個按鍵可以按的話，代表接下來如果讓兩個玩家繼續按下去要嘛就是按到同一個、要嘛就是按到鄰近的兩個，所以我們就要停下來。

Boundary Cases 處理

相信大家看到這裡應該心理面已經有怎麼解的動畫圖了。

我於是就按照上面這個想法來實作，可是丟出去馬上就會遇到 Wrong Answer，仔細看一下出問題的 input 才發現原來 vectors 可能會是空的。

怎麼辦? 好不容易用視覺化的工具了，怎麼可以因為這一點點特例就放棄?

當然我們還是要維護可讀性，我才不想用一大堆 if else 去專門處理這些 boundary cases。我們其實可以用 "想像的" index 來去讓 vectors 永遠都不可能是空的:


如果兩個 vectors 前後都加上最小和最大的數字，並不會影響到答案的正確性。

當然我沒有要去真的加這些數字進 vectors，在實務上這常常造成 side effects 所以我也很討厭新增東西進去再刪除的技巧。不要動 inputs 就對了!

不能動 inputs 我們可以動 index。所以當 index == -1 或 index == nums.size() 的話我在一個專門拿 vector 第幾個元素的 function 來回傳最小或最大的數字。

最後的程式碼就會長這樣:


class Solution {
 public:
  double findMedianSortedArrays(std::vector<int> &nums1,
                                std::vector<int> &nums2) {
    int topLineIndex1 = -1;
    int topLineIndex2 = -1;
    int bottomLineIndex1 = (int)nums1.size();
    int bottomLineIndex2 = (int)nums2.size();

    while (topLineIndex1 < bottomLineIndex1 ||
           topLineIndex2 < bottomLineIndex2) {
      const int num1Top = _getArrayNum(nums1, topLineIndex1);
      const int num2Top = _getArrayNum(nums2, topLineIndex2);
      const int num1Bottom = _getArrayNum(nums1, bottomLineIndex1);
      const int num2Bottom = _getArrayNum(nums2, bottomLineIndex2);

      // Find the smallest number on the top line
      if (num1Top < num2Top) {
        topLineIndex1++;
      } else {
        topLineIndex2++;
      }

      // Find the biggest number on the bottom line
      if (num1Bottom > num2Bottom) {
        bottomLineIndex1--;
      } else {
        bottomLineIndex2--;
      }
    }

    const int num1Top = _getArrayNum(nums1, topLineIndex1);
    const int num2Top = _getArrayNum(nums2, topLineIndex2);
    const int num1Bottom = _getArrayNum(nums1, bottomLineIndex1);
    const int num2Bottom = _getArrayNum(nums2, bottomLineIndex2);

    const int smallestNumOnTopLine = (num1Top < num2Top) ? num1Top : num2Top;
    const int biggestNumOnBottomLine =
        (num1Bottom > num2Bottom) ? num1Bottom : num2Bottom;

    return (smallestNumOnTopLine + biggestNumOnBottomLine) / 2.0;
  }

 private:
  int _getArrayNum(const std::vector<int> &nums, const int index) {
    if (index < 0) return -1000001;
    if (index >= (int)nums.size()) return 1000001;
    return nums.at(index);
  }
};

是不是很平鋪直敘?

延伸到多個 Vectors

以上的輔助工具其實還有一個好處，那就是其實他可以不只解決兩個 vectors 的題目。三個 vectors? 四個 vectors? 好多 vectors? 全部都可以用同一種解法。

像是三個 vectors 我們可以這樣想:


就只是把線條變成有關節的線條了，作法還是一樣沒變，我們每次都往另外一端找最快會點到的按鍵，再把線條移動。

優化速度

用 Callgrind 技巧分析了一下就會發現 code 大部分時間都花在 vector 的 access 上:


所以如果真的要優化程式碼我們可以做以下的 tricks:

  • 把 vector 提早轉換成 array，因為 vector 最多也才 1000 個 elements，但是 while 迴圈會頻繁的存取 elements
  • 把 vector::at() 存取改成 vector[] 因為有人說這樣比較快
  • 不要用另外一個 function 來去做 boundary case 的檢查，直接用 ? : 寫死在 while 迴圈裏面
  • 有動到 index 的人我才去把對應的 number 更新，不然原本作法每 iterate 一次其實一定會有一個 number 是不會變化的

光聽了就覺得很可怕，看了優化後的程式會更可怕:


class Solution {
 public:
  double findMedianSortedArrays(std::vector<int> &nums1Vector,
                                std::vector<int> &nums2Vector) {
    const int *nums1 = nums1Vector.data();
    const int *nums2 = nums2Vector.data();

    int topLineIndex1 = -1;
    int topLineIndex2 = -1;
    const int m = (int)nums1Vector.size();
    const int n = (int)nums2Vector.size();
    int bottomLineIndex1 = m;
    int bottomLineIndex2 = n;

    int num1Top = (topLineIndex1 < 0
                       ? -1000001
                       : (topLineIndex1 >= m ? 1000001 : nums1[topLineIndex1]));
    int num2Top = (topLineIndex2 < 0
                       ? -1000001
                       : (topLineIndex2 >= n ? 1000001 : nums2[topLineIndex2]));
    int num1Bottom =
        (bottomLineIndex1 < 0
             ? -1000001
             : (bottomLineIndex1 >= m ? 1000001 : nums1[bottomLineIndex1]));
    int num2Bottom =
        (bottomLineIndex2 < 0
             ? -1000001
             : (bottomLineIndex2 >= n ? 1000001 : nums2[bottomLineIndex2]));
    while (topLineIndex1 < bottomLineIndex1 ||
           topLineIndex2 < bottomLineIndex2) {
      // Find the smallest number on the top line
      if (num1Top < num2Top) {
        topLineIndex1++;
        num1Top = (topLineIndex1 < 0
                       ? -1000001
                       : (topLineIndex1 >= m ? 1000001 : nums1[topLineIndex1]));
      } else {
        topLineIndex2++;
        num2Top = (topLineIndex2 < 0
                       ? -1000001
                       : (topLineIndex2 >= n ? 1000001 : nums2[topLineIndex2]));
      }

      // Find the biggest number on the bottom line
      if (num1Bottom > num2Bottom) {
        bottomLineIndex1--;
        num1Bottom =
            (bottomLineIndex1 < 0
                 ? -1000001
                 : (bottomLineIndex1 >= m ? 1000001 : nums1[bottomLineIndex1]));
      } else {
        bottomLineIndex2--;
        num2Bottom =
            (bottomLineIndex2 < 0
                 ? -1000001
                 : (bottomLineIndex2 >= n ? 1000001 : nums2[bottomLineIndex2]));
      }
    }

    const int smallestNumOnTopLine = (num1Top < num2Top) ? num1Top : num2Top;
    const int biggestNumOnBottomLine =
        (num1Bottom > num2Bottom) ? num1Bottom : num2Bottom;

    return (smallestNumOnTopLine + biggestNumOnBottomLine) / 2.0;
  }
};

想要改 code 的人: wut?

重跑了一次 Callgrind 發現的確時間是有變少，如果我把 IR 排序的話會看到 % 數少很多:


可是丟到 LeetCode 上發現時間並沒有變化多少，他的時間有時候快到 20ms 慢到 80ms 都有可能，而且丟優化的並沒有感覺差多少:

(看起來很快? 其實只是僥倖這麼快的)

有時候我們提早優化程式或是 "我們以為" 這樣做會變快，可是實際上跑起來根本差不多，優化過後的 code 又極度犧牲了可讀性。我就寧願他慢一點，好維護比較重要，要優化隨時都可以做。

以上的 code 和 design spec 我都放在 GitHub 上了，如果有興趣的話歡迎參考。

延伸閱讀

下一篇我們來繼續用節奏遊戲的概念講解 O(log(m+n)) 的演算法。

留言

發佈留言

此網誌的熱門文章

[試算表] 追蹤台股 Google Spreadsheet (未實現損益/已實現損益)

-
圖片
在 Dcard 上發了一篇文結果引起超多網友回應想要看試算表，我就來整理一下我追蹤台股用的 Google 試算表給大家。 這個試算表我目標是以 "簡單" 為主，底下我也會講解公式的運作原理，希望大家能以此試算表輕鬆擴充自己想要的功能。 功能 未實現損益 (Unrealized Gain/Loss 表) 不管同一支股票是不是有部分已經賣出，只要你還持有未賣出的股票這邊都看的到。 已實現損益 (Realized Profit/Loss 表) 我過去的績效如何? 在這個表一目了然。 未實現損益: 詳細資料 (Unrealized Stats 表) 我還持有多少股? 每股市值多少? 每股的成本是多少? 在這個表可以快速追蹤。 手機友善 (Mobile Friendly) 我為了在手機上也可以快速看我想看的資訊，把 "Unrealized Gain/Loss" 做成比較窄的版型。 只要下載 Google Sheets app 打開試算表就可以了。 Google Spreadsheet 連結 Google Drive 連結 Stock Tracking 使用方式 請先點 "檔案" -> "建立副本"，copy 一份試算表到你自己的 Google Drive 將 "Current Price" 表單中填上你想要追蹤的股票代號和名稱 將 "Transactions" 表單中刪除範例資料，但請務必留下第 2 列 (因為有公式)，然後慢慢往下填入你的資料 Step 1: 檔案 -> 建立副本 Step 2: 新增/刪除股票代號和名稱 (紅框圈起處)，灰色底欄位代表有公式 Step 3: 在 "Transactions" 表填入資料到白色底欄位 (紅框圈起處)，灰色底欄位代表要讓公式自動計算 未實現損益的正確算法 其實在發 Dcard 文之前我自己也像 另外一個表單 犯了同樣的錯誤，就是只有在股票全部賣光光 (持有 0 股) 後計算的未實現損益才會正確。還沒全部賣光怎麼辦? 難道就不顯示了嗎? 飲料的例子 只要股票中途賣出一部分，目前還持有部分股票的話，感覺計算就突然變得很複雜。但不用怕，我們來用飲料當作股票舉個超簡單的例子 (1 杯=1...
閱讀更多

[Side Project] 互動式教學神經網路反向傳播 Interactive Computational Graph

-
圖片
成品 互動式網頁連結:  Interactive Computational Graph 微積分課經典的範例 df/dx sin(x) / x: 2 個 inputs, 1 個 output, 沒有 hidden layer 的 fully connected neural network: 為何要做這套工具 以前在學 machine learning 的時候覺得最難理解的部分就是 backpropagation，也就是神經網路到底是怎麼用數學來做訓練的。 我們知道神經網路就是長這樣子: Source: Wikipedia 但實際上每個 neuron (圓圈圈) 裡面有許多基本的數學運算，像是 sum 還有 activation function: Source:  Neural Networks and Machine Learning 當我們把所有東西綜合在一起，腦袋就會打結，到底 chain rule 是怎麼在這麼複雜的神經網路之間套用的? 就算了解基礎也很難相信實際上到底怎麼運作的。我又沒有要真的使用的話，網路上的教學就覺得看看就好 Source:  A Step by Step Backpropagation Example 但決心要了解 backpropagation 細節之後，不少教學都提到了 computational graph，從基礎的數學運算當作 nodes 來去理解似乎是比較簡單的方式。 後來找到了這篇文章  Calculus on Computational Graphs: Backpropagation  把 chain rule 講解的簡單至極，於是就在想，為何我不做一個網頁，讓大家可以自由地組合想要的 graph，然後看一下 chain rule 是怎麼流通的。 失敗作經驗 在做這次 side project 前，其實早在一年前我就開始作另一個 side project 是想展現神經網路的訓練過程。名稱叫做 explain-derivatives，是被 TensorFlow 的一個網頁 A Neural Network Playground 啟發的。 但由於一開始欠缺規劃，想到什麼就加什麼功能進去，造成架構一直修改，最後由於程式碼架構太過複雜就放棄了。 這個 project 是用 Cy...
閱讀更多

[插件] 在 Chrome 網頁做區分大小寫的搜尋

-
圖片
寫軟體的時候最常用到的功能就是上網查 API 文件，但是常常會遇到一個困擾就是，搜尋的文字在 Chrome 裡面是不區分大小寫 (case-insensitive) 的。有的時候是還好，多按一些 F3 就找到了，可是有時候實在是太多大小寫的東西混在一起，這時候我們有一些快速的解法: 用 Firefox 搜尋 (Firefox 的搜尋框裡面預設就提供有 match case 的功能了) 開 DevTools 按 Ctrl + Shift + F 進行全部東西的搜尋 (不過大概會發瘋) 用插件的解法算是意外發現的，原本只是在找有沒有可以用 regex 搜尋的插件，沒想到意外發現  regex 的插件也是可以拿來做區分大小寫 (case-sensitive) 的一般搜尋。 用 Chrome Regex Search 來做區分大小寫的搜尋 先裝好 Chrome Regex Search 之後，按 Ctrl + Shift + F 或是點工具列的圖示，打上想找的文字就可以了。 例如我最近在看 Qt QTextCursor 的文件，但是我只想找 "cursor"，很不幸的如果用 Chrome 預設搜尋他會把一大堆 QText Cursor 也會找到: 如果用 Chrome Regex Search 就會侷限在小寫的 "cursor": 用 Regex 的陷阱 如果你不知道 regex 是什麼，那你很有可能會發現在搜尋一些含特殊符號的東西會搜尋到怪怪的東西，不然就是搜尋會失敗。 這是因為 regex 本來就是偏工程師在用的東西，有一些符號是有特殊涵意的，所以如果搜尋的字包含以下任何特殊符號記得要在前面加一個反斜線 \ ( ref ): . + * ? ^ $ ( ) [ ] { } | \ 例如我想搜尋 1+1=(2-1)+1*1 ，那其實要打 1\+1=\(2-1\)\+1\*1  才會正確找的到。 是不是很麻煩? 不過如果你要找的東西有特殊符號的話，其實用一般 Chrome 的搜尋通常是不會有太多搜尋結果的，那就用一般搜尋就好。 Chrome 什麼時候要支援大小寫搜尋? 其實上面弄了那麼麻煩，還不如開個 Firefox 搜尋更快。那我就滿好奇，這麼基本的功能怎麼 Chrome 一直都沒做? 找了一下才發現 Super User 有人...
閱讀更多