文章

顯示從 5月, 2021 起發佈的文章

[LeetCode] 更快的 Recursion?! 用 Divide-and-Conquer 解 #10 Regular Expression Matching

-
圖片
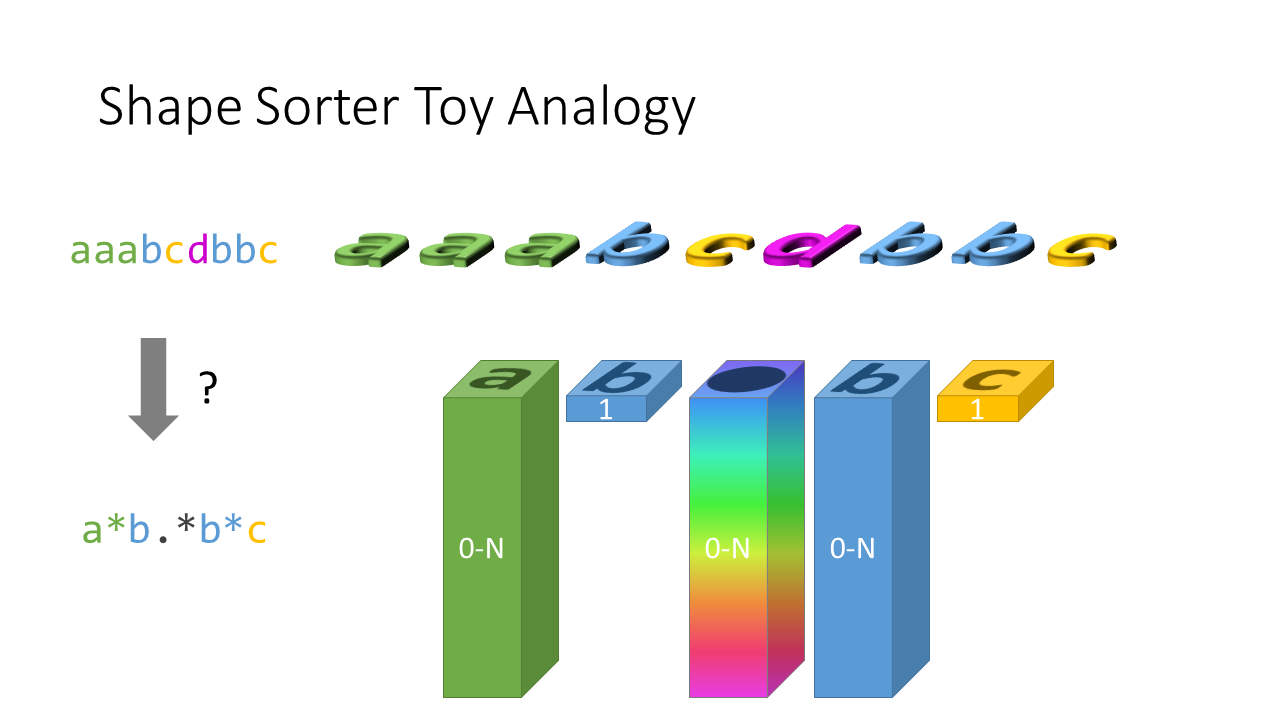
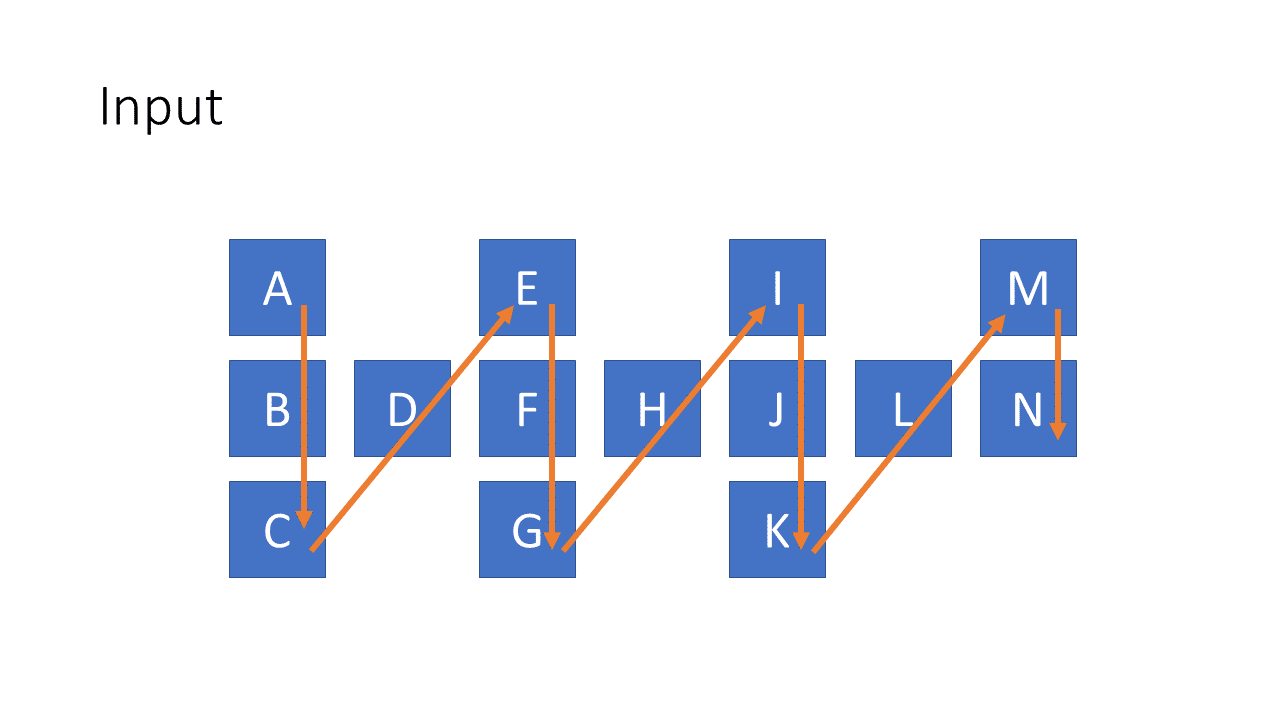
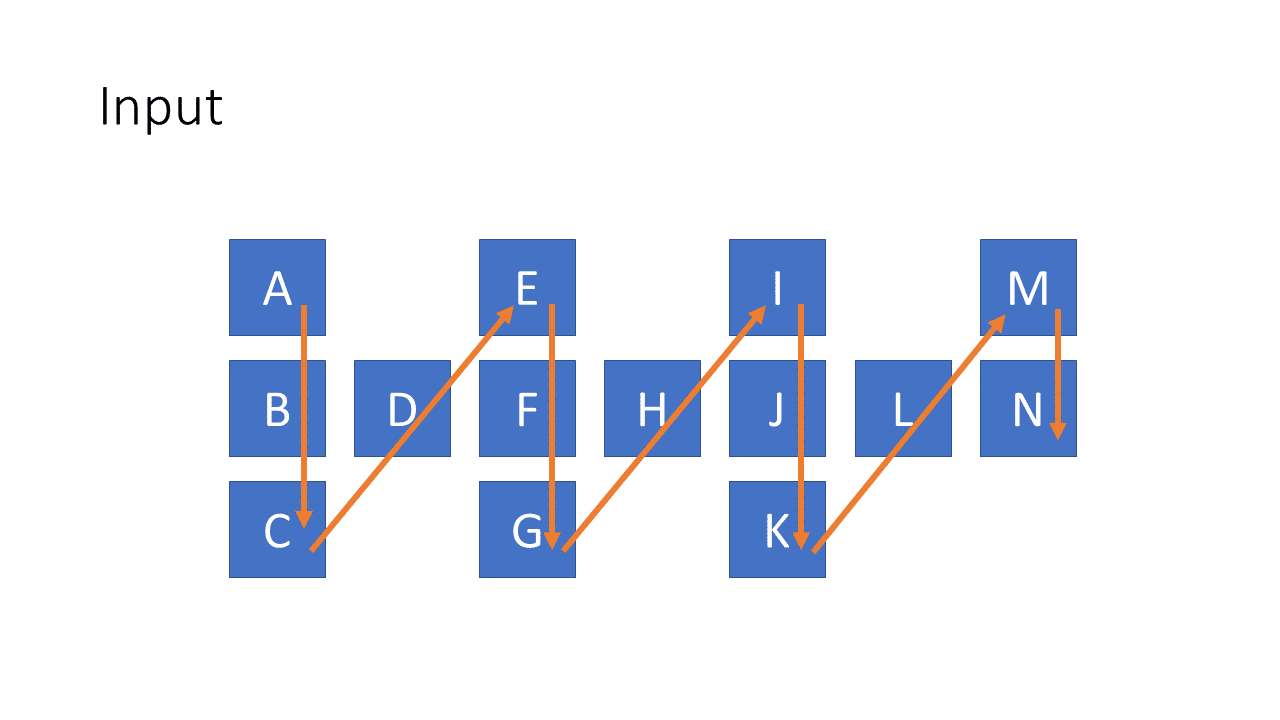
這題幾乎所有解答不是用從左往右的 Recursion 來解就是 DP 解。但我這次要用從中間開始的 Recursion 來追上 DP 的速度。 直覺的比喻 寶寶最愛玩的形狀配對盒今天要來幫助我們解題了! 為什麼我會想到用這個比喻就是之前看了一個 Reddit " Devs watching QA test the product " 一個幽默影片裡面就惡搞寶寶最愛玩的形狀配對盒子，把所有積木都丟到正方形孔去。 假設今天我們要把 " aaabcdbbc " 這串 s 測試能不能 match 一段 regular expression " a*b.*b*c "。 有 " * " 符號的我們就用一個什麼都裝的下的積木盒來代表、沒有 " * " 符號的我們用只能裝下 1 個積木的積木盒代表: 所以題目問的就是: 我們可以從左往右依序丟積木，符合積木盒上的數目要求嗎? 這樣丟就可以了: 什麼時候會失敗? 你沒丟完的時候，別想把積木藏起來: 或是有積木盒沒丟到數目要求: 但不是每一個積木盒都要丟，" x* " 類型的積木盒你不丟也無所謂: 為何不能遇到 * 就狂丟 LeetCode 第一個解答是從左往右丟積木，遇到 " x* " 的積木盒，要嘛就是丟一個要嘛就是不丟，因為後面會發生什麼事還不知道，都試試看再說。 為什麼我們遇到 " x* " 會沒辦法決定要不要丟? 舉個例子像是 s = "aaa", p = "a*a" ，如果你把 3 個 " a " 都丟到 p[0:1] 的 " a* " 那最後面的 " a " 要誰來 match? 這時候 greedy 反而會失敗，所以你只能試所有的可能性。 各個擊破 (Divide and Conquer) 有點像 Quicksort，我們先取中間的 character 找到適合的積木盒丟下去: 不過要記得每個可能性都還是要試過。要從左往右或隨機挑就隨便你了。 接著我們問說左邊剩下的 input string 可以被 match 嗎? 再問右邊可以被 match 嗎? 就這樣
發佈留言
閱讀更多

[LeetCode] 懶惰但不用 string 來解 #9 Palindrome Number

-
圖片
反轉數字就解完了 如果用字串解我們當然很直覺就想反轉字串，既然題目 "Follow up" 那邊不希望我們用字串，那我們就把數字當字串來反轉，就可以得到超乾淨的解答: class Solution { public: bool isPalindrome(int x) { if (x < 0) return false; return x == reverse(x); } int reverse(int x) { int output = 0; while (x != 0) { const int digit = x % 10; output *= 10; output += digit; x /= 10; } return output; } }; Overflow! 只是解完前幾題之後我們大概對 int 範圍都很敏感了，我們知道任意對 int 操作很容易讓他超出 [INT_MIN, INT_MAX] 的範圍，所以我們在還沒 submit 之前就大概知道上面這個解會 overflow 壞掉。 如果你看過 #7 或 #8 我的解答你可能會猜說這作者到底有什麼強迫症就是要在 int 限制下偵測 overflow，是不是又要搬出什麼 safeMultiply, safeAdd。 可是既然題目只問我能不能不要轉成 string 來解題: 當然可以啊，那我把上面 code 改一下，不轉 string 我轉 long 就不用麻煩去偵測 overflow 了: class Solution { public: bool isPalindrome(int x) { if (x < 0) return false; return (long)x == reverse(x); } long reverse(int x) { long output = 0; while (x != 0) { const int digit = x % 10; output *= 10; output += digit; x /= 10;
發佈留言
閱讀更多

[LeetCode][C++] 用乾淨簡單的方式解 #8 String to Integer (atoi)

-
圖片
這題 Acceptance rate 是 LeetCode 前幾名最低的，只有 16% 左右，看似複雜但其實可以變成很簡單，只要我們把問題切成小塊來處理就好了。 何謂 Read In? 有沒有發現題目描述提到很多次 "Read in"? 其實每次 Read in 就是把一個 character 給吃掉的意思: 在 Parse 字串的時候有時候你會想要吃掉 character，有時候卻又不想吃掉。像是如果突然讀到一個數字字元 "4"，但這時候還在決定正負號怎麼辦? 那當然就是不要吃掉這個字元，留給負責處理數字的步驟去處理。 Easy As 123 既然題目描述都跟你說 1、2、3 步要做什麼了，我們可以就寫相對應的 functions 一個專心處理一件事就好。 第一步我們先看看要不要狂吃空白字元，認不得的東西就算了丟給第二步: 這邊如果你看到我標示的 "Read" 亮框就表示每走過一次箭頭就應該要把一個字元吃掉。 第二步我們來看看正負號，決定最後到底是正是負: 第三步我們就狂吃數字字元，直到沒辦法再吃為止: 如果看了這三張投影片，我們不管用什麼程式語言應該都可以寫出 code 來了。 如果我用 C++ 寫就會寫出像這樣的 code: class Solution { public: int myAtoi(std::string s) { int index = 0; while (runStep1(s, index /*may change*/)) ; while (runStep2(s, index /*may change*/)) ; while (runStep3(s, index /*may change*/)) ; if (!m_positive) m_result *= -1; return m_result; } bool runStep1(const std::string &s, int &index) { if (index >= s.size()) return false; if (s.at(index) == ' ') {
發佈留言
閱讀更多

[LeetCode][C++] 只用 int 來實作 #7 Reverse Integer

-
圖片
我知道很多人都用 string 或 long 來做這題，雖然很簡單卻沒辦法學到這題的關鍵。 LeetCode 官方解答 用了一個很 tricky 的方式偵測 overflow/underflow 恐怕也不是很通用的解。 題目的關鍵 把數字反轉根本不是重點，如果我真的要反轉數字我這樣寫就好了: class Solution { public: int reverse(int x) { int output = 0; while (x != 0) { const int digit = x % 10; output *= 10; output += digit; x /= 10; } return output; } }; 結束? 但題目希望你單純用 int 來解，而且如果結果超出 int 範圍又要 return 0，這代表我們只能用 int 來偵測甚麼時候數字會超出 int 範圍。 先了解一下 C++ Overflow/Underflow 會發生什麼事? 這就跟用什麼語言來寫非常有關係了，所以我查了一下看到這個 StackOverflow 解答 才知道原來 C++ 在執行像是 a + b 如果超出範圍的話 (overflow) 什麼狀況都有可能發生 (undefined behavior)，意味這程式已經沒救了，比 crash 還糟糕因為 a + b 有可能是任何數字。 C++ compiler 其實還有 內建的 overflow 檢查 像是  __builtin_add_overflow 來偵測什麼時候 overflow，不過我們為了學到點什麼當然不能拿來作弊。 那我們到底要怎麼偵測 a + b 會不會爆掉? 我們只要會數學的移項就好了。 移項 我們今天想偵測 a + b 是不是大於 int 最大值 (overflow)，或偵測 a + b 是不是小於 int 最小值 (underflow)，我們想知道會不會爆掉就這樣寫: return (a + b) > INT_MAX; // overflow return (a + b) < INT_MIN; // underflow 很可惜 C++ 在做左邊的 a + b 時早就爆了，這時我們就可以很聰明的把
發佈留言
閱讀更多

[LeetCode] 把 #6 ZigZag Conversion 當作蛇一樣，用圖像來解題

-
圖片
上一篇文章 我們用了 Table 方式來嘗試解題，但程式碼有點複雜而且還比較慢。 我後來想了一下，原來我們只要畫蛇添足就可以用最快最省記憶體的方式來解這題！ 畫蛇添足法 因為題目說要擺成這個方式，我們就真的要乖乖擺成這樣嗎? 這就讓我想到之前有 9 個點要你畫 4 條直線的 思考遊戲 ，雖然我也滿討厭那個解答，不過我得說他可能貢獻了 8.7% 讓我想到下面這個方法: 如果我們把它擺成這樣方方正正的有什麼好處呢? 我們可以繼續用上一篇的 Table 方法 來解: 只是這次我們非常好判斷什麼時候他會變成 '\0' 了，主要就是因為變成方方正正的。 唯一的例外就是每個字串的第一個頭，就把他想成蛇的頭好了。 我們只要 col=0~N, row=0~M 慢慢一個一個拜訪，然後再轉成像蛇在走路的 index 去讀 s 就行了: 看到這邊我相信你應該不用什麼複雜的 index 分析就知道該怎麼解了吧? C++ 程式碼 根據上面投影片來實作，我們應該可以得到像下面這樣的程式碼: class Solution { public: std::string convert(std::string s, int numRows) { if (numRows <= 1) return s; const int numCols = s.size() / (numRows - 1) + 1; std::string output; for (int r = 0; r < numRows; r++) { for (int c = 0; c < numCols; c++) { const int snakeIndex = getSnakeIndex(r, c, numRows); const char ch = getChar(s, snakeIndex, numRows); if (ch != '\0') output += ch; } } return output; } private: char getChar(const std::string &s, const int snakeInd
發佈留言
閱讀更多

[LeetCode] 用 Table 來解 #6 ZigZag Conversion

-
圖片
LeetCode #6 官網的 解答 第一個其實就很好了解，所以似乎這題看起來沒必要寫文章? 但我就想用一些原創、網路上找不到的方法、又簡單的把他解掉。 題目與解法 例如他把一疊標記 ABCD... 的卡片擺成這樣: 你要從左到右，從上到下的順序把卡片重新排列輸出: 當然我第一個想到的就是用 table 的方式讓他把字串擺進我的 table 中，我再來從左到右、從上到下慢慢掃就結束啦。 最後再把 "*" 的字元刪掉就好了。 因為我們變成 table 所以我們需要知道 table 的寬度才能正確計算從 2D 變成 1D 的 index，我們其實可以把它變成一個一個 group 來算: 程式碼 所以 C++ 程式碼就會長這樣: #include <algorithm> class Solution { public: std::string convert(std::string s, int numRows) { if (numRows == 1) return s; const int numColumns = calcNumColumns(s, numRows); std::string output(numRows * numColumns, '*'); int row = 0, col = 0; bool goingDown = true; for (const char c : s) { const int index = row * numColumns + col; output[index] = c; row += (goingDown ? 1 : -1); col += (goingDown ? 0 : 1); if (row == 0) goingDown = true; if (row == numRows - 1) goingDown = false; } output.erase(std::remove(output.begin(), output.end(), '*'), output.end()); return ou
發佈留言
閱讀更多

[LeetCode] 用對稱圖形來理解 Manacher's Algorithm #5 Longest Palindromic Substring

-
圖片
Manacher's Algorithm 被大家形容得好像是很困難的演算法。於是我在想，有沒有辦法把 Manacher's Algorithm 用好玩的方式來理解呢? 更簡單的演算法可以參考 上一篇文章 。 理解 Manacher's Algorithm 對稱半徑 回文相對於圖片就是對稱圖形的概念，我們今天的目標就是找法國、加拿大、法國國旗組在一起裡面最寬的對稱圖形: 如果我們這樣切，每個地方都可以當摺線，我們可以說對稱的地方半徑是 2: 因為往左或往右都有 2 塊。 沒有對稱的地方就是 0: 當然還有另外一種對稱是不看中間的那塊，像是文字 "aba" 我們就可以不看 "b"，像是我們可以忽略楓葉中間那塊: 對稱中的對稱 (Case 1) 這大概就是 Manacher's Algorithm 裡面最核心的概念。 假設我們已經知道有一塊半徑是 6 的對稱，如果左邊有一小塊半徑 1 的對稱，那我們可以知道右邊的對稱半徑嗎? 如果你把左半邊連數字和箭頭也當圖片的話，那右半邊不就長的一樣? 那半徑也就一樣? 沒錯，這種感覺就好像蝴蝶翅膀上面比較小的圈圈自然也會對稱在另外一邊: 被砍掉的對稱 (Case 2) 那如果有對稱超過藍色對稱的範圍怎麼辦? 像是這樣: 既然藍色對稱的範圍只到那邊，就代表他的外面一定不一樣，我們當然不能 copy 左半邊的半徑: 真可惜，不過我們會發現，我們還是可以把右半邊往中間擠到藍色對稱範圍裏面就可以對稱了: 可以更寬的對稱 (Case 3) 我們再來看最後一個 case，如果左半邊剛好碰到邊緣會發生什麼事? 這邊我把加拿大國旗中間一小塊換成藍色的: 的確這和 Case 1 看起來好像沒什麼差別，一樣的對稱半徑，But... 我們如果把右半邊的對稱稍微拉長一下，會發現，哇，右半邊有可能變更長耶，左半邊卻是沒辦法: Manacher's Algorithm 設計是當碰到這個情形就把藍色的中心點移到這個新的地方繼續跑，因為我們還沒讀到右邊邊界外，沒人知道他會變多長，這只能繼續乖乖左右慢慢拉開嘗試。 所以 Manacher's Algorithm 比 O(n^2) 演算法聰明的地方就只有重複利用上面藍色對稱的部分裡面的資訊，只要超出這個範圍，很抱歉就只好一個一個字元比
發佈留言
閱讀更多

此網誌的熱門文章

[試算表] 追蹤台股 Google Spreadsheet (未實現損益/已實現損益)

-
圖片
在 Dcard 上發了一篇文結果引起超多網友回應想要看試算表，我就來整理一下我追蹤台股用的 Google 試算表給大家。 這個試算表我目標是以 "簡單" 為主，底下我也會講解公式的運作原理，希望大家能以此試算表輕鬆擴充自己想要的功能。 功能 未實現損益 (Unrealized Gain/Loss 表) 不管同一支股票是不是有部分已經賣出，只要你還持有未賣出的股票這邊都看的到。 已實現損益 (Realized Profit/Loss 表) 我過去的績效如何? 在這個表一目了然。 未實現損益: 詳細資料 (Unrealized Stats 表) 我還持有多少股? 每股市值多少? 每股的成本是多少? 在這個表可以快速追蹤。 手機友善 (Mobile Friendly) 我為了在手機上也可以快速看我想看的資訊，把 "Unrealized Gain/Loss" 做成比較窄的版型。 只要下載 Google Sheets app 打開試算表就可以了。 Google Spreadsheet 連結 Google Drive 連結 Stock Tracking 使用方式 請先點 "檔案" -> "建立副本"，copy 一份試算表到你自己的 Google Drive 將 "Current Price" 表單中填上你想要追蹤的股票代號和名稱 將 "Transactions" 表單中刪除範例資料，但請務必留下第 2 列 (因為有公式)，然後慢慢往下填入你的資料 Step 1: 檔案 -> 建立副本 Step 2: 新增/刪除股票代號和名稱 (紅框圈起處)，灰色底欄位代表有公式 Step 3: 在 "Transactions" 表填入資料到白色底欄位 (紅框圈起處)，灰色底欄位代表要讓公式自動計算 未實現損益的正確算法 其實在發 Dcard 文之前我自己也像 另外一個表單 犯了同樣的錯誤，就是只有在股票全部賣光光 (持有 0 股) 後計算的未實現損益才會正確。還沒全部賣光怎麼辦? 難道就不顯示了嗎? 飲料的例子 只要股票中途賣出一部分，目前還持有部分股票的話，感覺計算就突然變得很複雜。但不用怕，我們來用飲料當作股票舉個超簡單的例子 (1 杯=1
閱讀更多

[Side Project] 互動式教學神經網路反向傳播 Interactive Computational Graph

-
圖片
成品 互動式網頁連結:  Interactive Computational Graph 微積分課經典的範例 df/dx sin(x) / x: 2 個 inputs, 1 個 output, 沒有 hidden layer 的 fully connected neural network: 為何要做這套工具 以前在學 machine learning 的時候覺得最難理解的部分就是 backpropagation，也就是神經網路到底是怎麼用數學來做訓練的。 我們知道神經網路就是長這樣子: Source: Wikipedia 但實際上每個 neuron (圓圈圈) 裡面有許多基本的數學運算，像是 sum 還有 activation function: Source:  Neural Networks and Machine Learning 當我們把所有東西綜合在一起，腦袋就會打結，到底 chain rule 是怎麼在這麼複雜的神經網路之間套用的? 就算了解基礎也很難相信實際上到底怎麼運作的。我又沒有要真的使用的話，網路上的教學就覺得看看就好 Source:  A Step by Step Backpropagation Example 但決心要了解 backpropagation 細節之後，不少教學都提到了 computational graph，從基礎的數學運算當作 nodes 來去理解似乎是比較簡單的方式。 後來找到了這篇文章  Calculus on Computational Graphs: Backpropagation  把 chain rule 講解的簡單至極，於是就在想，為何我不做一個網頁，讓大家可以自由地組合想要的 graph，然後看一下 chain rule 是怎麼流通的。 失敗作經驗 在做這次 side project 前，其實早在一年前我就開始作另一個 side project 是想展現神經網路的訓練過程。名稱叫做 explain-derivatives，是被 TensorFlow 的一個網頁 A Neural Network Playground 啟發的。 但由於一開始欠缺規劃，想到什麼就加什麼功能進去，造成架構一直修改，最後由於程式碼架構太過複雜就放棄了。 這個 project 是用 Cytoscape.js 為底，加上 TypeScr
閱讀更多

[插件] 在 Chrome 網頁做區分大小寫的搜尋

-
圖片
寫軟體的時候最常用到的功能就是上網查 API 文件，但是常常會遇到一個困擾就是，搜尋的文字在 Chrome 裡面是不區分大小寫 (case-insensitive) 的。有的時候是還好，多按一些 F3 就找到了，可是有時候實在是太多大小寫的東西混在一起，這時候我們有一些快速的解法: 用 Firefox 搜尋 (Firefox 的搜尋框裡面預設就提供有 match case 的功能了) 開 DevTools 按 Ctrl + Shift + F 進行全部東西的搜尋 (不過大概會發瘋) 用插件的解法算是意外發現的，原本只是在找有沒有可以用 regex 搜尋的插件，沒想到意外發現  regex 的插件也是可以拿來做區分大小寫 (case-sensitive) 的一般搜尋。 用 Chrome Regex Search 來做區分大小寫的搜尋 先裝好 Chrome Regex Search 之後，按 Ctrl + Shift + F 或是點工具列的圖示，打上想找的文字就可以了。 例如我最近在看 Qt QTextCursor 的文件，但是我只想找 "cursor"，很不幸的如果用 Chrome 預設搜尋他會把一大堆 QText Cursor 也會找到: 如果用 Chrome Regex Search 就會侷限在小寫的 "cursor": 用 Regex 的陷阱 如果你不知道 regex 是什麼，那你很有可能會發現在搜尋一些含特殊符號的東西會搜尋到怪怪的東西，不然就是搜尋會失敗。 這是因為 regex 本來就是偏工程師在用的東西，有一些符號是有特殊涵意的，所以如果搜尋的字包含以下任何特殊符號記得要在前面加一個反斜線 \ ( ref ): . + * ? ^ $ ( ) [ ] { } | \ 例如我想搜尋 1+1=(2-1)+1*1 ，那其實要打 1\+1=\(2-1\)\+1\*1  才會正確找的到。 是不是很麻煩? 不過如果你要找的東西有特殊符號的話，其實用一般 Chrome 的搜尋通常是不會有太多搜尋結果的，那就用一般搜尋就好。 Chrome 什麼時候要支援大小寫搜尋? 其實上面弄了那麼麻煩，還不如開個 Firefox 搜尋更快。那我就滿好奇，這麼基本的功能怎麼 Chrome 一直都沒做? 找了一下才發現 Super User 有人
閱讀更多