[LeetCode] 不用 Stack 改用 Recursion 來解 #20 Valid Parentheses

- 7月 04, 2021

如果面試出這題我大概會說，阿不就用 stack，網路上隨便一找也如出一轍都用 stack。那如果不給你用 stack 呢?

何謂合法的一堆括號

LeetCode 解答一堆文字我真的覺得和上課或教科書沒兩樣，以前上課也是被灌輸這就是要用 stack，可是為什麼要用 stack? 之前的人怎麼知道的?

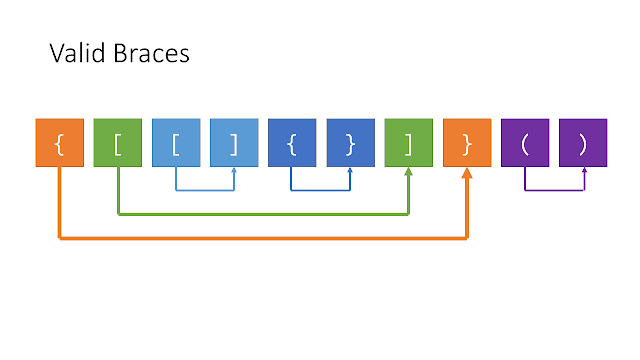
我們就用圖片來理解一下比較快:

如果我們把左邊和右邊的括號用一條線連起來，我們會發現他有一種把俄羅斯娃娃拆開放的感覺。

題目問是不是 valid，其實就是問拆開放的俄羅斯娃娃能不能組的回去? 說不定有人偷了一小塊，或是順序亂掉了就會變 invalid。

我也有點懶得做俄羅斯娃娃的圖片，所以我們直接來看一些 invalid 的範例:

最常見的 invalid 大概是第一個，我們把括號交錯放，如果不用 stack 就會誤判是 valid。

其他常見的 invalid 是找不到右邊的括號，或是左邊的括號不見了。

用 Stack 來做

為什麼大家這麼喜歡用 stack 來做這一題? 因為我們發現從左到右的順序剛好可以用 stack 的 push & pop 來代表:

任何破壞 stack 操作這樣 push & pop 的人都是 invalid。

我們按照這想法來寫一個很簡單的 C++ code 就會變成:


class Solution {
 public:
  bool isValid(std::string s) {
    std::stack<char> leftParens;
    for (int i = 0; i < s.size(); i++) {
      const char c = s.at(i);
      if (isLeftParen(c)) {
        leftParens.push(c);
      } else {
        if (leftParens.empty()) return false;
        const char prevC = leftParens.top();
        leftParens.pop();
        if (!isPair(prevC, c)) return false;
      }
    }
    return leftParens.empty();
  }

  bool isPair(const char c1, const char c2) {
    return (c1 == '(' && c2 == ')') || (c1 == '[' && c2 == ']') ||
           (c1 == '{' && c2 == '}');
  }

  bool isLeftParen(const char c) { return c == '(' || c == '[' || c == '{'; }
};

括號數量那麼少，我們就不用特地開一個 map 來記錄括號種類，反而會弄得很複雜。

不用 Stack 怎麼辦?

突然變超難

假設我們遇到一些技術性問題，剛好全部類似 stack 的東西就無法用，我們又趕著做出可以跑的程式怎麼辦?

被 stack 寵壞的我們就開始緊張了，天啊，怎麼可能不用 stack?

可是我們後來就可以想到，recursive call 遞迴呼叫其實也是一種 stack，說不定我們改一下變成 recursion 就解決了。我一開始也是這樣想，但實際開始做才發現真的有夠困難。

如果我們用 stack 資料結構，最後一個 element 有可能是對應到 recursive call 是好幾個之前的 function，我們要怎麼存取資料? 就變得有點困難，我們也不想用一些 vector 或 stack 的 containers 來當作 arguments，不然就直接用純 stack 解法就好了，何必這麼麻煩?

用類似 Parsing 的技巧

但我們換個想法，用類似 DFA 的做法:

我們設計一個 function，先看第一個 index 的字元是不是左括號，是的話再比較右邊的 index 的字元是什麼情況。

只有右邊的字元是另外一個左括號我們才需要繼續 recursive call 下去，其他狀況我們可以當下判斷是不是 valid。

Recursive call 的感覺就會變成這樣:

這個 recursive function 總共被呼叫了 3 次，我們還要記得回傳下一個開始要掃描的 index 在哪。

另外一個狀況是如果 recursive function 一開始就碰到右括號的話，那當然很直截了當我們就知道是 invalid:

一開始我其實有點懶得去處理 index 的問題所以還寫了這樣的 C++ code 去修改 string，把判斷完的 substring 刪除，但是 91 個 test case 就剛好發現最後一個 test case 太長會造成 TLE:

我們單純用 stack 來做要故意製造 TLE 應該是滿困難的，改個寫法就可以立刻碰到 TLE 真的意想不到。

所以我就想說，好吧看來還是要乖乖去操作 index，一直去修改 string 太慢了。於是用同個想法，但是換個寫法:


class Solution {
 public:
  bool isValid(std::string s) {
    int leftIndex = 0, rightIndex = 1, nextIndex = 0;
    while (leftIndex < s.size()) {
      if (!eat(s, leftIndex, rightIndex, nextIndex /*change*/)) return false;
      leftIndex = nextIndex;
      rightIndex = leftIndex + 1;
    }
    return true;
  }

  bool eat(const std::string &s, const int leftIndex, const int rightIndex,
           int &nextIndex /*change*/) {
    if (leftIndex >= s.size() || rightIndex >= s.size()) return false;
    const char leftChar = s.at(leftIndex);
    const char rightChar = s.at(rightIndex);
    if (!isLeftParen(leftChar)) return false;
    if (isRightParen(rightChar) && !isPair(leftChar, rightChar)) return false;
    if (isPair(leftChar, rightChar)) {
      nextIndex = rightIndex + 1;
      return true;
    } else {
      if (!eat(s, rightIndex, rightIndex + 1, nextIndex /*change*/))
        return false;
      return eat(s, leftIndex, nextIndex, nextIndex /*change*/);
    }
  }

  bool isPair(const char c1, const char c2) {
    return (c1 == '(' && c2 == ')') || (c1 == '[' && c2 == ']') ||
           (c1 == '{' && c2 == '}');
  }

  bool isLeftParen(const char c) { return c == '(' || c == '[' || c == '{'; }

  bool isRightParen(const char c) { return c == ')' || c == ']' || c == '}'; }
};

老實說真的滿複雜的，但我 Clean Code 能力可能還有所不足，希望大家可以寫出比我 clean 的程式碼。

Submit 完就得到和 stack 版本差不多的結果:

創意 Python 解法

我在討論區看到一個很創意的解法，他直接從最小的左右括號慢慢刪除:


class Solution(object):
    def isValid(self, s):
        while "()" in s or "{}" in s or '[]' in s:
            s = s.replace("()", "").replace('{}', "").replace('[]', "")
        return s == ''

真的超簡潔的，雖然這解法應該是 O(N^2) 因為最慘的狀況就是每次都要掃完 string 一次，每次也才移除一個 "()"。N + (N-2) + (N-4) + ... 梯形公式算一下還是 N^2。

因為上面已經有修改 string 會造成 TLE 的經驗了，如果我不去做 replace 只把字元變成空白會不會比較快一點? 我就試著用 C++ 來做做看:


class Solution {
 public:
  bool isValid(std::string s) {
    while (eat(s))
      ;
    for (const char c : s) {
      if (c != ' ') return false;
    }
    return true;
  }

  bool eat(std::string &s) {
    bool hasEat = false;
    int prevIndex = 0;
    for (int i = 0; i < s.size(); i++) {
      const char c = s.at(i);
      if (c == ' ') continue;
      const char prevC = s.at(prevIndex);
      if (isPair(prevC, c)) {
        s[prevIndex] = ' ';
        s[i] = ' ';
        hasEat = true;
      }
      prevIndex = i;
    }
    return hasEat;
  }

  bool isPair(const char c1, const char c2) {
    return (c1 == '(' && c2 == ')') || (c1 == '[' && c2 == ']') ||
           (c1 == '{' && c2 == '}');
  }
};

結果雖然慢很多但至少可以過:

結語

再簡單的題目其實還是可以用截然不同的好幾種方式去解決，說不定也能在一些特殊場合上派上用場。

這次我們就自己來設計一套不用 stack 的新演算法，也能看到有些狀況下 stack 真的不適合改成 recursion，讓可讀性大幅下降其實沒什麼好處。

如果面試被問到如何用 recursion，我大概也沒辦法立刻想出來。但也請不要拿去用在面試上，我們還是想要乾淨的 code。

搜尋此網誌

Clean Code Craving